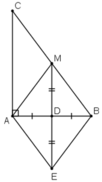
Cho tam giác ABC vuông tại A, trung tuyến AM, D là trung điểm của AB.Gọi E là điểm đối xứng với M qua D, F là điểm đối xứng với A qua M.
a) Tứ giác AEMC là hình gì ? Vì sao ?
b) Chứng minh: tứ giác ABFC là hình chữ nhật.
c) Chứng minh: AB ⊥ BM
d) Biết AB = 6cm, BC = 10cm. Tính diện tứ giác ABFC