2. Hãy chỉ ra độ dài đáy và đường cao tương ứng trong mỗi hình tam giác vuông sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


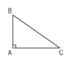
a) Trong tam giác ABC:
- Coi AC là đáy thì AB là đường cao.
- Coi AB là đáy thì AC là đường cao.
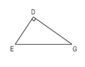
b) Trong tam giác DEG:
- Coi DE là đáy thì GD là đường cao.
- Coi DG là đáy thì ED là đường cao.

- Trong tam giác ABC: AB là đáy, CH là đường cao.
- Trong tam giác DEG: EG là đáy, DK là đường cao.
- Trong tam giác MPQ: PQ là đáy, MN là đường cao.
Nói thêm:
- Mỗi tam giác có góc tù sẽ có hai đường cao nằm ngoài tam giác.
- Mỗi tam giác vuông đều có hai đường cao chính là hai cạnh góc vuông.

- Trong tam giác ABC: AB là đáy, CH là đường cao.
- Trong tam giác DEG: EG là đáy, DK là đường cao.
- Trong tam giác MPQ: PQ là đáy, MN là đường cao.
Nói thêm:
- Mỗi tam giác có góc tù sẽ có hai đường cao nằm ngoài tam giác.
- Mỗi tam giác vuông đều có hai đường cao chính là hai cạnh góc vuông.

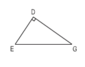
Trong tam giác DEG:
- Coi DE là đáy thì GD là đường cao.
- Coi DG là đáy thì ED là đường cao.

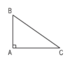
Trong tam giác ABC:
- Coi AC là đáy thì AB là đường cao.
- Coi AB là đáy thì AC là đường cao.

Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)
Hình 1: Đáy AC, đường cao BA
Hình 2. Đáy DE, DG , đường cao DG, DE.
where is the triangles ???????????????