Cho hình vuông abcd cạnh a. Trên cạnh BC lấy E và trên tia BC lấy F sao cho BE.BF = a^2. Gọi H là giao của DC và AE.
a) Tìm giá trị nhỏ nhất của AE.AH.
b) CMR: CH=CF
c) Gọi I là giao điểm của đường thẳng DE và BH. CMR: CI vuông góc AH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DC
0
Những câu hỏi liên quan
CM
12 tháng 4 2018
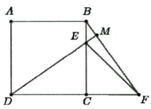
Chứng minh được:
C B F ^ + B E M ^ = M D F ^ + D E C ^ = 90 0
=> B M D ^ = 90 0 nên M thuộc đường tròn đường kính BD. Mà E Î BC nên quỹ tích của điểm M là là cung B C ⏜ của đường tròn đường kính BD
27 tháng 5 2022
△AOE và △BOG có:
\(AO=BO\) (O là tâm hình vuông ABCD).
\(AE=BG\)
\(\widehat{OAE}=\widehat{OBG}=45^0\)
\(\Rightarrow\)△AOE=△BOG (c-g-c).
\(\Rightarrow OE=OG;\widehat{AOE}=\widehat{BOG}\)
Mà \(\widehat{AOE}+\widehat{BOE}=90^0\) \(\Rightarrow\widehat{GOE}=\widehat{BOG}+\widehat{BOE}=90^0\)
\(\Rightarrow\)△OGE vuông cân tại O.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)
18 tháng 1 2023
a: Xét ΔAFD vuông tại D và ΔAEB vuông tại B có
AD=AB
góc FAD=góc EAB
Do đó: ΔAFD=ΔAEB
b: ΔAFD=ΔAEB
=>AF=AE
=>ΔAFE cân tại A
mà AI là trung tuyến
nên AI vuông góc với EF
Xét ΔINE vuông tại I và ΔIMF vuông tại I có
IE=IF
góc IEN=góc IFM
Do đó: ΔINE=ΔIMF
=>IN=IM
Xét tứ giác MFNE có
I là trung điểm chung của MN và FE
MN vuông góc với FE
Do đó: MFNE là hình thoi
