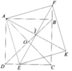
cho hình vuông ABCD, Trên cạnh DC lấy diểm M, tia đối BC lấy N sao cho BN=DM
a) chứng minh tam giác AMN vuông cân .
b) gọi O là trung điểm MN. Chứng minh B,O,D thẳng hàng
c) F đối xứng A qua O. Chứng minh tứ giác ANFM là hình vuông
mk cần gấp lắm giúp mình câu 2 nhé!!
arigatou