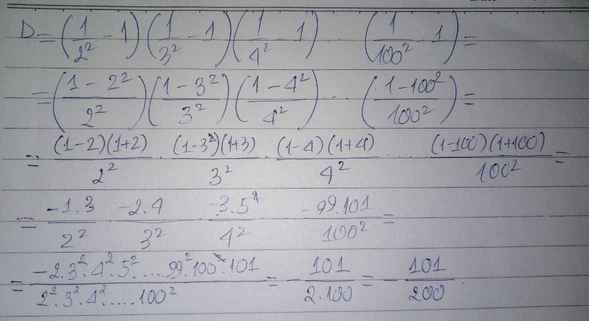Tính:\(E=1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+\dfrac{1}{4}\left(1+2+3+4\right)+...+\dfrac{1}{100}\left(1+2+...+100\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 3 2021
Ta thấy \(1-\dfrac{1}{n^2}=\dfrac{\left(n-1\right)\left(n+1\right)}{n^2}\) với mọi \(n>0\).
Từ đó \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)...\left(1-\dfrac{1}{100^2}\right)=\dfrac{1.3}{2^2}.\dfrac{2.4}{3^2}...\dfrac{99.101}{100}=\left(\dfrac{1}{2}.\dfrac{2}{3}...\dfrac{99}{100}\right).\left(\dfrac{3}{2}.\dfrac{4}{3}...\dfrac{101}{100}\right)=\dfrac{1}{100}.\dfrac{101}{2}=\dfrac{101}{200}\).
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2023
Ta có:
\(1-\dfrac{1}{1+2+...+n}=1-\dfrac{1}{\dfrac{n\left(n+1\right)}{2}}=\dfrac{n\left(n+1\right)-2}{n\left(n+1\right)}=\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow S=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{99.102}{100.101}\)
\(=\dfrac{1.2.3...99}{2.3.4...100}.\dfrac{4.5.6...102}{3.4.5...101}=\dfrac{1}{100}.\dfrac{102}{3}=\dfrac{17}{50}\)
27 tháng 6 2022
1: \(S=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot\dfrac{5}{4}\cdot...\cdot\dfrac{101}{100}=\dfrac{101}{2}\)
2: \(B=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2006}{2007}=\dfrac{1}{2007}\)
11 tháng 7 2018
\(S=1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+\dfrac{1}{4}\left(1+2+3+4\right)+...+\dfrac{1}{100}\left(1+2+3+...+100\right)\)
\(=1+\dfrac{1}{2}.\dfrac{2\left(1+2\right)}{2}+\dfrac{1}{3}.\dfrac{3\left(1+3\right)}{2}+\dfrac{1}{4}.\dfrac{4\left(1+4\right)}{2}+...+\dfrac{1}{100}.\dfrac{100\left(1+100\right)}{2}\)
\(=1+\dfrac{2\left(1+2\right)}{2.2}+\dfrac{3\left(1+3\right)}{2.3}+\dfrac{4\left(1+4\right)}{2.4}+...+\dfrac{100\left(1+100\right)}{2.100}\)
\(=1+\dfrac{1+2}{2}+\dfrac{1+3}{2}+\dfrac{1+4}{2}+...+\dfrac{1+100}{2}\)
\(=1+\dfrac{3+4+5+...+101}{2}\)
\(=1+\dfrac{\dfrac{99\left(101+3\right)}{2}}{2}\)
\(=1+2574=2575\)
\(\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 2 2021
Áp dụng \(1+2+...+n=\dfrac{n\left(n+1\right)}{2}\)
\(\Rightarrow\dfrac{1}{n}\left(1+2+...+n\right)=\dfrac{n\left(n+1\right)}{2n}=\dfrac{n+1}{2}\)
Vậy:
\(A=\dfrac{1}{2}+\dfrac{3}{2}+\dfrac{4}{2}+...+\dfrac{101}{2}=\dfrac{1+2+3+...+100}{2}-1\)
\(=\dfrac{100.101}{2}-1=5049\)
