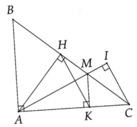
Bài 1. Cho tam giác ABC vuông tại A, kẻ đường phân giác BM. Trên cạnh BC lấy
điểm D sao cho BD = BA.
a) Chứng minh BM AD .
b) Gọi H là hình chiếu vuông góc của D trên AC, K là hình chiếu vuông góc của
A trên DM. Chứng minh ba đường thẳng AK, BM, DH đồng quy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chú ý tam giác ABD cân tại B nên BM là đường phân giác cũng là đường cao, từ đó B M ⊥ A D .
b) Chú ý AK, BM, DH là ba đường cao của tam giác AMD.

a: góc AHC=góc AKC=90 độ
=>AHKC nội tiếp
b: Sửa đề; AB*HC=AC*HA
Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>AB*HC=AC*HA

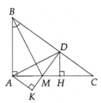
Bài 1:
Do E là hình chiếu của D trên AB:
=) DE\(\perp\)AB tại E
=) \(\widehat{DE\text{A}}\)=900
Do F là hình chiếu của D trên AC:
=) DF\(\perp\)AC
=) \(\widehat{DFA}\)=900
Xét tứ giác AEDF có :
\(\widehat{D\text{E}F}\)=\(\widehat{E\text{A}F}\)=\(\widehat{DFA}\) (cùng bằng 900)
=) Tứ giác AEDF là hình chữ nhật
Xét hình chữ nhật AEDF có :
AD là tia phân giác của \(\widehat{E\text{A}F}\)
=) AEDF là hình vuông

1: Xét tứ giác AMDN có
góc AMD=góc AND=góc MAN=90 độ
AD là phan giác
=>AMDN là hình vuông
2: BC=căn 3^2+4^2=5cm
AD là phân giác
=>DB/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7
=>BD=15/7cm; CD=20/7cm