Question

[Trịnh Khoa]

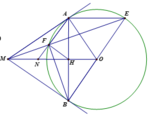
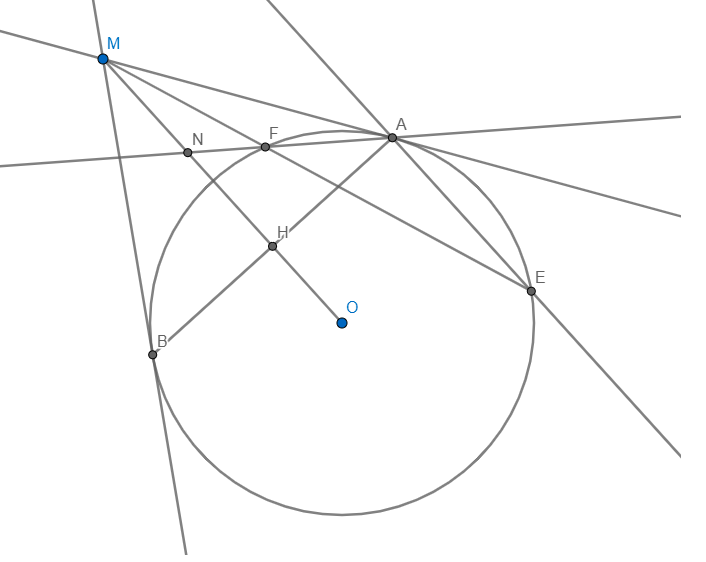
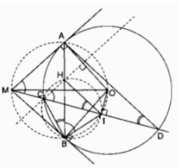
cho đường tròn tâm O bán kính R. Từ 1 điểm M ở ngoài đường tròn, kẻ hai tiếp tuyến MA và MB với đường tròn. Qua A kẻ đường thẳng song song với MO cắt đường tròn tại , đường thẳng ME cắt đường tròn tại F, đường thẳng AF cắt MO tại N, H là giao điểm của MO và AB. a) chứng minh: tứ giác MAOB nội tiếp đường tròn.

b)chứng minh: MA.AB=2MH.AO

Answer 1

[Đỗ Minh Đức Anh]

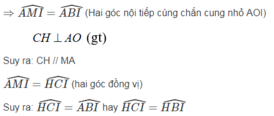
a) Chứng minh tứ giác MAOB nội tiếp đường tròn
Xét tứ giác MAOB có: \(\widehat{MAO}=90\text{°}\) (MA là tiếp tuyến của (O)); \(\widehat{MBO}=90\text{°}\) (MB là tiếp tuyến của (O))
→ \(\widehat{MAO}+\widehat{MBO}=180\text{°}\)
mà \(\widehat{MAO}\) và \(\widehat{MBO}\) là hai góc đối nhau
→ Tứ giác MAOB nội tiếp (dhnb) (đpcm)

b) Chứng minh MA.AB = 2MH.AO
Ta có: OA = OB (A, B ∈ (O))
→ O thuộc đường trung trực của AB (1)
Lại có: MA = MB (Tính chất hai tiếp tuyến cắt nhau)
→ M thuộc đường trung trực của AB (2)
Từ (1) và (2) → OM là đường trung trực của AB
→ OM ⊥ AB tại H và H là trung điểm của AB
→ \(\widehat{MHA}=90\text{°}\) và AB = 2AH
Xét ∆MAO và ∆MHA có: \(\widehat{MAO}=\widehat{MHA}=90\text{°}\); \(\widehat{M}\) chung
→ ∆MAO ∼ ∆MHA (g.g) → \(\dfrac{MA}{MH}=\dfrac{AO}{HA}\) (cặp cạnh tương ứng)
→ MA.HA = MH.AO
→ 2MA.HA = 2MH.AO
Mà AB = 2AH (cmt) → MA.AB = 2MH.AO (đpcm)

Answer 2

[Wuynh Ha Vii]

 MA.HA = MH.AO
→ 2MA.HA = 2MH.AO
Mà AB = 2AH (cmt) → MA.AB = 2MH.AO (đpcm) 
chỗ đây ko hiểu ;;;-;;;