trong mặt phẳng với hệ tọa độ Oxy, cho đường trong (C) \(x^2+y^2-4x+6y-12=0\) và D(1,1). Đường thẳng( \(\Delta\)) đi qu và cắt (C) tại hai điểm phân biệt A, B sao cho độ dài đoạn AB nhỏ nhất có phương trình dạng x+by+c=0 ( b, c thuộc Z).Tính b+2c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 12 2019
Chọn đáp án C
Mặt cầu (S) có tâm I(4;3;3) và bán kính R = 4. Gọi I’ là hình chiếu của I trên mặt phẳng α .
Đường thẳng I I ' đi qua I(4;3;3) và nhận n = ⇀ 1 ; 1 ; 1 làm vectơ chỉ phương nên có phương trình là:
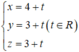
Tọa độ điểm I’ thỏa mãn hệ
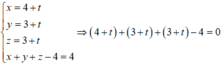
⇔ t = - 2 . Suy ra I’(2;1;1).
Gọi hình tròn (C) bán kính r là thiết diện của khối cầu (S) khi cắt bởi mặt phẳng α . Khi đó I’ là tâm của đường tròn (C).
Ta có I M = 14 < 4 = R và M ∈ α nên điểm M thuộc miền trong của đường tròn (C) (M nằm trong hình trong hình tròn).
Do đường thẳng d ⊂ α , d đi qua M và d cắt mặt cầu tại hai điểm A, B nên d cắt đường tròn (C) tại hai điểm A, B.
Phương tích của điểm M với đường tròn (C): M A . M B = r 2 - I ' M 2 .
Do r không đổi nên r 2 - I ' M 2 không đổi ⇒ M A . M B không đổi.
Lại có
Dấu “=” xảy ra khi MA = MB hay A B ⊥ M I ' .
Mà A B ⊥ M I ' nên đường thẳng AB có một vectơ chỉ phương là u ⇀ = I I ' ; ⇀ M I ' ⇀ = 2 ; - 4 ; 2 (cùng phương với vectơ u 2 ⇀ )
CM
23 tháng 6 2018
Đáp án C
có tâm I(4;3;3) bán kính R =4
Gọi phương trình đường thẳng d có dạng
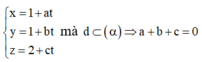
Khoảng cách từ tâm I đến d là
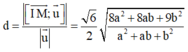
Ta có
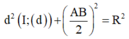
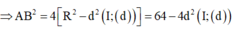
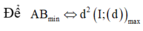
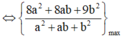
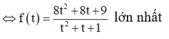
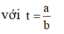
Khi đó
7 tháng 5 2022
Đường tròn \((C)\) tâm \(I(a;b)\) bán kính \(R\)có phương trình
\((x-a)^2+(y-b)^2=R^2.\)
\(∆MAB ⊥ M\) \(\rightarrow \) \(AB\) là đường kính suy ra \(∆\) qua \(I\) do đó:
\(a-b+1=0 (1)\)
Hạ \(MH⊥AB\) có \(MH=d(M, ∆)= \dfrac{|2-1+1|}{\sqrt{2}}={\sqrt{2}} \)
\(S_{ΔMAB}=\dfrac{1}{2}MH×AB \Leftrightarrow 2=\dfrac{1}{2}2R\sqrt{2} \)
\(\Rightarrow R = \sqrt{2} \)
Vì đường tròn qua\(M\) nên (\(2-a)^2+(1-b)^2=2 (2)\)
Ta có hệ :
\(\begin{cases} a-b+1=0\\ (2-a)^2+(1-b)^2=0 \end{cases} \)
Giải hệ \(PT\) ta được: \(a=1;b=2\).
\(\rightarrow \)Vậy \((C) \)có phương trình:\((x-1)^2+(y-2)^2=2\)
HP
19 tháng 6 2021
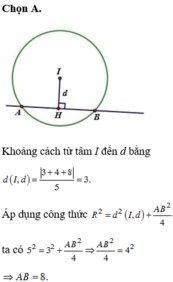
\(\left(C\right):x^2+y^2+4x-6y-12=0\)
\(\Leftrightarrow\left(C\right):\left(x+2\right)^2+\left(y-3\right)^2=25\)
\(\Rightarrow I=\left(-2;3\right)\) là tâm đường tròn, bán kính \(R=5\)
Kẻ IH vuông góc với AB.
\(\Rightarrow IH=\sqrt{R^2-AH^2}=\sqrt{5^2-\dfrac{1}{4}.50}=\dfrac{5\sqrt{2}}{2}\)
Đường thẳng AB có dạng: \(ax+by-2a=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;AB\right)=\dfrac{\left|-2a+3b-2a\right|}{\sqrt{a^2+b^2}}=\dfrac{5\sqrt{2}}{2}\)
\(\Leftrightarrow7a^2-48ab-7b^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=7b\\b=-7a\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}AB:7x+y-14=0\\AB:x-7y-2=0\end{matrix}\right.\)
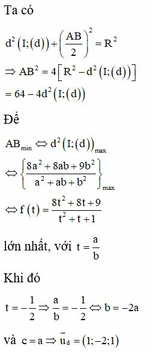
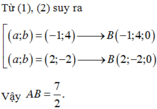
(C) là đường tròn tâm \(I\left(2;-3\right)\) bán kính \(R=5\)
\(\overrightarrow{DI}=\left(1;-4\right)\Rightarrow ID=\sqrt{17}< R\Rightarrow\) D là 1 điểm thuộc miền trong đường tròn
Gọi H là hình chiếu vuông góc của I lên \(\Delta\Rightarrow\) H là trung điểm AB
Theo định lý Pitago: \(AH^2=IA^2-IH^2=R^2-IH^2\Leftrightarrow\dfrac{1}{4}AB^2=25-IH^2\)
\(\Rightarrow AB\) đạt min khi và chỉ khi IH đạt max
Mặt khác trong tam giác vuông IDH, theo định lý đường xiên-đường vuông góc ta luôn có:
\(IH\le ID\Rightarrow IH_{max}=ID\) khi H trùng D \(\Leftrightarrow\Delta\perp ID\)
\(\Rightarrow\) đường thẳng \(\Delta\) nhận (1;-4) là 1 vtpt
Phương trình \(\Delta\):
\(1\left(x-1\right)-4\left(y-1\right)=0\Leftrightarrow x-4y+3=0\)
\(\Rightarrow\left\{{}\begin{matrix}b=-4\\c=3\end{matrix}\right.\)