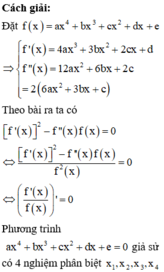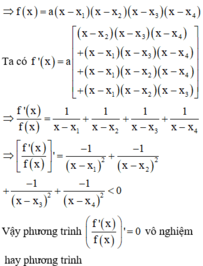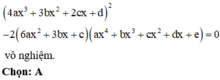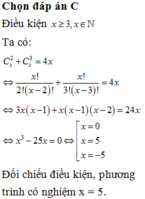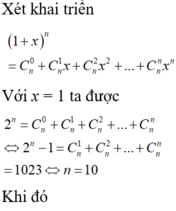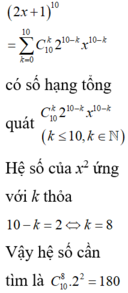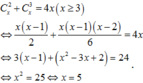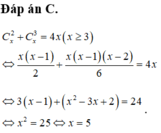AX101 + Bx11 + cx2 = 243
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
TM
28 tháng 8 2017
\(\left(ax+b\right)\left(x^2-x-1\right)=ax^3+cx^2+1\)
\(\Leftrightarrow ax^3+\left(b-a\right)x^2+\left(-b-a\right)x-b=ax^3+cx^2+0.x+1\)
sử dụng đồng nhất thức ta được: \(\hept{\begin{cases}b-a=c\\-b-a=0\\-b=1\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=-1\\c=-2\end{cases}}\)
22 tháng 8 2021
ax2+cx2-ay+ay2-cy+cy2
= x2(a+c)-y(a+c)+y2(a+c)
= (a+c)(x2-y+y2)
CM
3 tháng 4 2018
Ta có
Đồ thị hàm số 
cắt trục hoành tại bốn điểm phân biệt bên phương trình 
, với 
là các nghiệm.
Suy ra
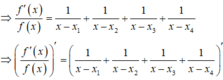
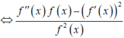
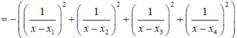
Nếu 
với 
thì 
, 
.
Nếu 
thì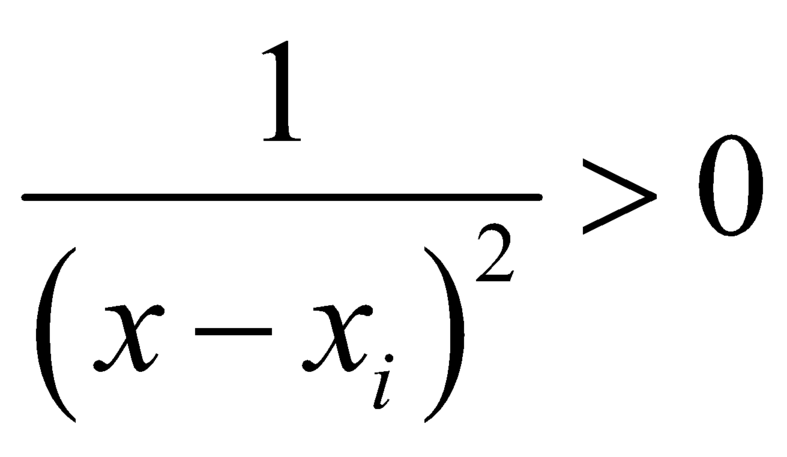 
, 
.
Suy ra 
.
Vậy phương trình 
vô nghiệm hay phương trình 
vô nghiệm.
Do đó, số giao điểm của đồ thị hàm số và trục hoành là 0
Đáp án A
CM
7 tháng 1 2017
Đáp án B
Giả thiết
Đặt
thì
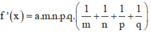
Và
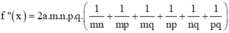
Khi đó, phương trình
(vô nghiệm)
Vậy đồ thị hàm số y = g(x) không cắt trục hoành.
