1 Nêu tính chất 3 đường trung tuyến , tia phân giác của một góc , đường phân giác của tam giác
2 Nêu cách chứng minh 3 điểm thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2022
Bài 1:
3 đường trung tuyến cắt nhau tại một điểm gọi là trọng tâm của tam giác
3 đường phân giác cắt nhau tại một điểm gọi là tâm đường tròn nội tiếp của tam giác
CM
23 tháng 10 2017
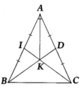
Vì tam giác ABC cân tại A nên tia phân giác AK đồng thời là đưòng trung tuyến.
Mà BD là trung tuyến của tam giác ABC nên K là trọng tâm của tam giác ABC.
Do đó I, K, C thẳng hàng
5 tháng 4 2018
+) Tính chất của đường trung trực của tam giác: 3 đường trung trực của tam giác cắt nhau tại 1 điểm; điểm đó cách đều 3 cạnh của tam giác đó.
+) Tính chất đường cao trong tam giác: 3 đường cao trong tam giác cắt nhau tại 1 điểm
+) Tính chất đường phân giác của tam giác: 2 đường phân giác của tam giác cắt nhau tại một điểm; điểm đó cách đều 3 cạnh của tam giác đó.
+) Tính chất đường trung tuyến của tam giác: 3 đường trung tuyền của tam giác cắt nhau tại một điểm; điểm đó cách mỗi đỉnh khoảng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
Chúc bn học tốt!!!!!!
12 tháng 1 2017
bài toán này cũng dễ mà,nó ra là ... thôi bạn tự là đ
6 tháng 11 2017
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
19 tháng 6 2020
tự kẻ hình nha
đặt AM là tia phân giác của BAC
xét tam giác ABM và tam giác ACM có
BAM=CAM(gt)
AB=AC(gt)
ABC=ACB(gt)
=> tam giác ABM= tam giác ACM(gcg)
=> BM=CM(hai cạnh tương ứng)
=> M là trung điểm của BC=> AM là trung tuyến
vì I là trung điểm AB=> CI là trung tuyến
vì BD giao AM tại K mà BD, AM là trung tuyến=> K là trọng tâm
mà CI là trung tuyến => K thuộc CI=> I,K,C thẳng hàng
