Tìm hai số biết rằng 2 lần số thứ nhất lớn hơn 3 lần số thứ hai là 9 và hiôu các bình phương của chúng bằng119
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 2 2019
Đáp án A
Gọi số thứ nhất là a; a ∈ N, số thứ hai là b; b ∈ N Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:
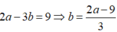
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:
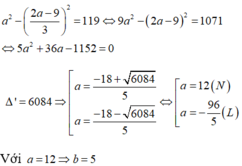
Vậy số lớn hơn là 12.
CM
27 tháng 2 2017
Đáp án A
Gọi số thứ nhất là a; a ∈ N , số thứ hai là b; b ∈ N
Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:
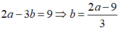
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:
a 2 – b 2 = 119 hay
a 2 − 2 a − 9 3 2 = 119 ⇔ 9 a 2 − 4 a 2 − 36 a + 81 = 119.9 ⇔ 5 a 2 + 36 a − 1152 = 0 T a c ó : Δ ' = 18 2 − 5. − 1152 = 6084 ⇒ Δ ' = 78
Nên phương trình có hai nghiệm
a 1 = − 18 − 78 5 = − 96 5 ( l o ạ i ) ; a 2 = − 18 + 78 5 = 12 ( n h ậ n )
⇒ b = 2.12 − 9 3 = 5
6 tháng 3 2023
a:
Sửa đề: Viết pt ẩn x,y
3x-4y=10 và x+y=36
b: 3x-4y=10 và x+y=36
=>3x-4y=10 và 3x+3y=108
=>-7y=-98 và x+y=36
=>y=14 và x=22
Lời giải:
Gọi hai số cần tìm là $a$ và $b$. Theo bài ra ta có:
\(\left\{\begin{matrix} 2a-3b=9\\ a^2-b^2=119\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2a=3b+9\\ (2a)^2-(2b)^2=476\end{matrix}\right.\)
\(\Rightarrow (3b+9)^2-4b^2=476\)
\(\Leftrightarrow 5b^2+54b-395=0\)
$\Leftrightarrow (b-5)(5b+79)=0$
$\Rightarrow b=5$ hoặc $b=-\frac{79}{5}$
Với $b=5$ thì $a=\frac{3b+9}{2}=12$
Với $b=\frac{-79}{5}$ thì $a=\frac{3b+9}{2}=\frac{-96}{5}$