Tìm số A biết số này được chia làm 3 phần tỉ lệ nghịch với 5;2;4 và tổng bình phương của 3 phần là 564
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi 3 phần là a,b,c
theo bài ra ta có: 5a=2b=4c
chia cả 3 cho bội chung nhỏ nhất ta có:5a/20=2b/20=4c/20
suy ra a/4=b/10=c/5 suy ra a^3/64=b^3/1000=c^3/125
Áp dụng tính chất dãy tỉ số = nhau ta có:
a^3/64=b^3/1000=c^3/125=(a^3+b^3+c^3)/64+1000+125=9512/1189=8
từ đó tìm dc 3 phần a,b,c rồi cộng lại dc số A

Gọi ba phần được chia ra từ số A lần lượt là x,y,z (x,y,z > 0)
Theo đề bài, ba phần tỉ lệ nghịch với các số nên ta có:
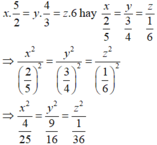
Tổng bình phương của ba phần là 24309 nên x 2 + y 2 + z 2 = 24309
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
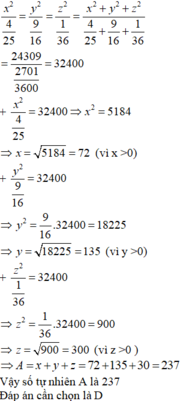

gọi 3 phần là a,b,c (a,b,c \(\in Q\)và a+b+c =A
ta có : 5a=2b=4c \(\Rightarrow\frac{a}{4}=\frac{b}{10}=\frac{c}{5}=\frac{a+b+c}{4+10+5}=\frac{a+b+c}{29}=k\left(k\ne0\right)\)(ad tc của dãy tỉ số = nhau )
\(\Rightarrow\left(\frac{a}{4}\right)^3=\left(\frac{b}{10}\right)^3=\left(\frac{z}{5}\right)^3=\frac{a^3+b^3+c^3}{64+1000+125}=\frac{9512}{1189}=8\)=k.k.k
(ad tc của dãy tso = nhau)
\(\Rightarrow k\in\left\{2\right\}\)
nếu k=2 thì A=2.29=58
VẬY A=58
Gọi x,y,z là 3 phần của a
Theo đề toán, ta có: 5x=2y=4z và x2+y2+z2=564
5x=2y=4z
=>\(\frac{5x}{20}=\frac{2y}{20}=\frac{4z}{20}\)(BCNN(5,2,4) = 20)
=> \(\frac{x}{4}=\frac{y}{10}=\frac{z}{5}\)
=>\(\frac{x^2}{16}=\frac{y^2}{100}=\frac{z^2}{25}\)
Áp dụng t/chất dãy tỉ số bằng nhau:
\(\frac{x^2}{16}=\frac{y^2}{100}=\frac{z^2}{25}=\frac{x^2+y^2+z^2}{16+100+25}=\frac{564}{141}=4\)
=> x2 = 4.16 = 64 => x = 8 hoặc -8
y2 = 4.100= 400 => y = 20 hoặc -20
z2 = 4.25 = 100 => z = 10 hoặc -10
tao ko bt làm