Hàm số f(x) được cho bởi công thức:
f(x)=4x-3+|5x-2|
Hãy viết hàm số f(x) dưới dạng không có giá trị tuyệt đối.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 10 2016
a ) Khi \(f\left(2\right)\)
\(5.2+1-\left|5.2-3\right|\)
\(=10+1-\left|10-3\right|\)
\(=10+1-7\)
\(=4\)
Khi \(f\left(-7\right)\)
\(5.\left(-7\right)+1-\left|2.\left(-7\right)-3\right|\)
\(=-35+1-\left|-14-3\right|\)
\(=-34-\left|-17\right|\)
\(=-34-17\)
\(=-51\)
13 tháng 10 2016
b ) Khi \(f\left(2\right)\) , thì :
\(5.2+1-2.2-3\)
\(=10+1-4-3\)
\(=4\)
Khi \(f\left(-7\right)\) , thì :
\(5.\left(-7\right)+1-2.\left(-7\right)-3\)
\(=-35+1+14-3\)
.\(=-23\)
CM
18 tháng 6 2017
Điền giá trị y = f(x) vào bảng sau:
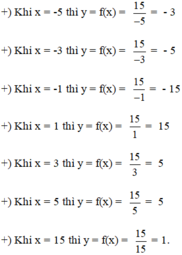
| x | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
| y=f(x) | -3 | -5 | -15 | 15 | 5 | 3 | 1 |
CM
27 tháng 12 2019
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
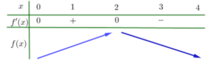
Từ bảng biến thiên, ta có nhận xét sau: 
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
BT
12 tháng 12 2017
Với mọi \(x\in R\) , ta có \(3x^2\ge0\) suy ra \(3x^2+5>5\). Vì vậy với mọi giá trị x thì hàm số đã cho nhận giá trị dương.
CM
3 tháng 2 2017
+) Dựa vào đồ thị ta có:
f(-2) = 3; f(1) = -1,5 và f(2)= -3
+) Kiểm tra lại bằng phép tính:
f(-2) = - 1,5. (-2)= 3.
f(1) = -1,5.1 = -1,5
f(2) = -1,5. 2 = - 3.
14 tháng 12 2017
ta có hàm số y = f(x) = 3x2 + 5
vì x2 \(\ge\)0 \(\forall\)x \(\Rightarrow\)3x2 + 5 \(\ge\)5 hay y \(\ge\)5
Vậy với mọi giá trị của x thì hàm số đã cho luôn nhận giá trị dương
14 tháng 12 2017
Vì x2>0 ( với mọi x ) nên 3x2+5 > 0
Vậy f(x) = 3x2 + 5 luôn nhận giá trị dương với mọi giá trị x ( đpcm ).
XONG RỒI ĐÓ...
4 tháng 12 2016
a)
+) x2 +2x + 1
f(-1) = (-1)2 + 2. (-1) + 1 = 1 + (-2) +1 = 0
f(1) = 12 +2 . 1 + 1 = 4
f(0) = 02 + 2.0 +1 = 1
b) y = 1
=> 1 = x2 + 2x + 1
=> x2 + 2x = 0
=> x . x + 2x = 0
=> x . ( x+2) = 0
=> x+ 2 = 0
=> x = -2
f(x)=4.(-3)+[-(5x-2)]
đúng ko
(chưa chắc đúng)
k đúng đâu cô giáo mk bảo x là đẳng thức,phải giải chi tiết ra