Cho tam giác ABC cân tại A kể AH vuông gốc BC ( H thuộc BC) Gọi I là trung điểm AC trên tia đối IB lấy K sao cho IB=IK cmr CK=AC AH cắt BI tại G kẻ CG cắt AB tại M.cmr MH//AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ABCD có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo BD
Do đó: ABCD là hình bình hành
b: Xét tứ giác AKCH có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo KH
Do đó: AKCH là hình bình hành
Suy ra: AK=HC

a) Xét △MIA và △BIH có
MI=BI( giả thiết)
góc MIA =góc BIH(2 góc đối đỉnh)
IA=IH(Vì I là trung điểm của AH)
=> △MIA = △BIH(c-g-c)
=>góc IMA=góc IBH (2 góc tương ứng)
hay góc BMA=góc MBH mà 2 góc này là 2 góc so le trong của đường thẳng MB cắt MA và BH
=>MA//BH
bạn tự làm câu b,c nhé

t lười vẽ hình lắm, vô cùng xin lỗi :(
a) Vì ∆ ABC cân tại A nên AH vừa là đường cao, vừa là trung tuyến => HB = HC = 12:2 = 6
Áp dụng định lí Py-ta-go cho ∆ AHB, ta được: AH2 + BH2 = AB2 => AB2 = 122 + 92 = 225 = 152 => AB = 15 = AC
=> PABC = AB + AC + BC = 15 + 15 + 18 = 48
b) Vì BM = CN (gt) ; HB = HC (cmt) => HB + BM = HC + CN => HM = HN => AH là trung tuyến của ∆ AMN (1)
Lại có: AH ┴ BC hay AH ┴ MN => AH là đường cao của ∆ AMN (2)
Từ (1) và (2) =>∆ AMN cân tại A
c) Xét ∆ BIM và ∆ CKN vuông tại I và K có:
MB = NC (gt) ; ^KNC = ^IMB (∆AMN cân tại A) => ∆ BIM = ∆ CKN ( ch - gn ) => MI = KN
Mà AM = AN (∆AMN cân tại A) => AI = AK => ∆ AIK cân tại A
=> ^AIK = ^AKI = ( 180o - ^MAN ) : 2 = ^AMN = ^ANM => IK // MN (đồng vị) hay IK // BC
d) Vì IK // MN => ^IKN = ^KCN (slt) ; ^KIB = ^IBM (slt)
Lại có: ^IBM = ^KCN ( vì ∆BIM=∆CKN ) => ^IKN = ^KIB hay ^OIK = ^OKI => ∆OKI cân tại O => OK = OI
Xét ∆ AIO và ∆ AKO có:
AI = AK ( ∆AIK cân tại A) ; OK = OI (cmt) ; AO (chung) => ∆ AIO = ∆ AKO ( c-c-c )
=> ^OAI = ^OAK (3)
Vì ∆AMN cân tại A => AH là phân giác của ∆AMN.=> ^HAM = ^HAN hay ^HAI = ^HAK (4)
Từ (3) và (4) => A, O, H thẳng hàng.
Ya, that's it!
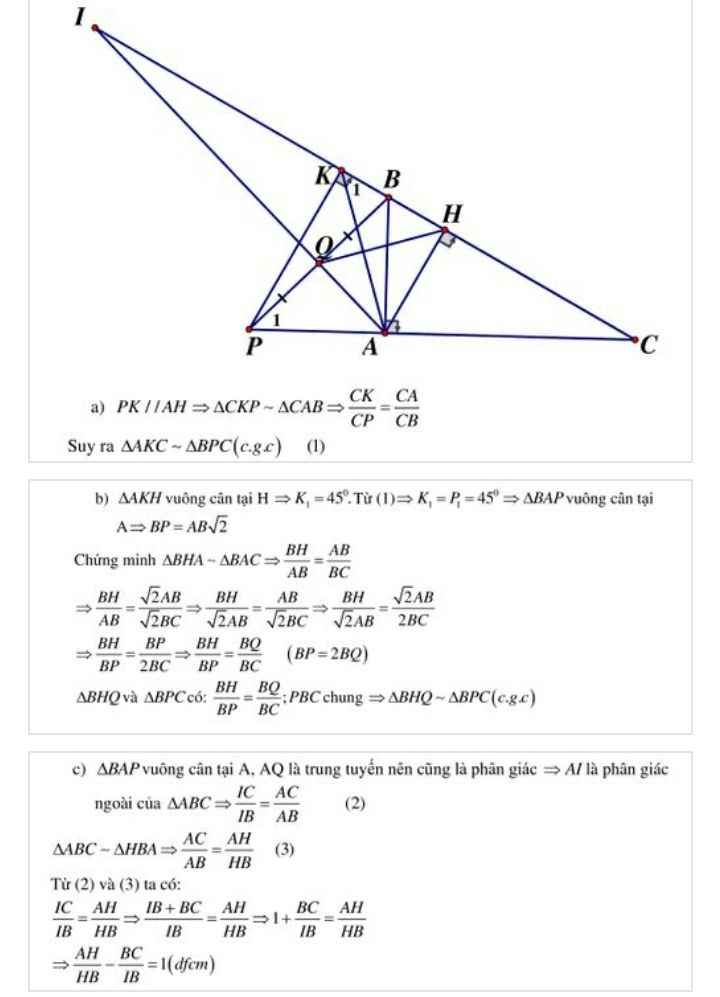

a) Chứng minh ΔAIB = ΔCIK (c - g - c)
=> Góc BAC = Góc ACK
Chứng minh ΔAIK = ΔCIB (c - g - c)
=> Góc CAK = Góc ACB
Xét tam giác ABC và tam giác ACK có:
Góc BAC = Góc ACK (cmt)
AC: chung
Góc CAK = Góc ACB (cmt)
=> Tam giác ABC = Tam giác CKA (c - g - c)
=> AC = CK (2 cạnh tương ứng)
b) Tam giác ABC có AH là đường trung tueyesn, BI là đường trung tueeys, AH và BI cắt nhau tại G
=> G là trọng tâm của tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}AG=\dfrac{2}{3}AH\\CG=\dfrac{2}{3}CM\end{matrix}\right.\)
Có; \(AG+GH=AH\)
\(\Rightarrow\dfrac{2}{3}AH+GH=AH\)
\(\Rightarrow GH=\dfrac{1}{3}AH\)
\(\dfrac{AG}{GH}=\dfrac{\dfrac{2}{3}AH}{\dfrac{1}{3}AH}=2\)
Chứng minh tương tự: \(\dfrac{CG}{MG}=2\)
\(\Rightarrow\dfrac{AG}{GH}=\dfrac{CG}{MG}\left(=2\right)\)
=> MH // AC