Câu 1: Cho tam giác ABC vuông tại A, vẽ tia phân giác BD của ABC ( D thuộc AC ). Trên cạnh BC lấy điểm E sao cho BE = AB. chứng minh rằng:
a) Tam giác ABD = tam giác EBD
b) Tính BED
c) Chứng minh tam giác BED vuông.
d) Vẽ AH vuông góc với BC. Chứng minh AH song song DE
Toán hình học

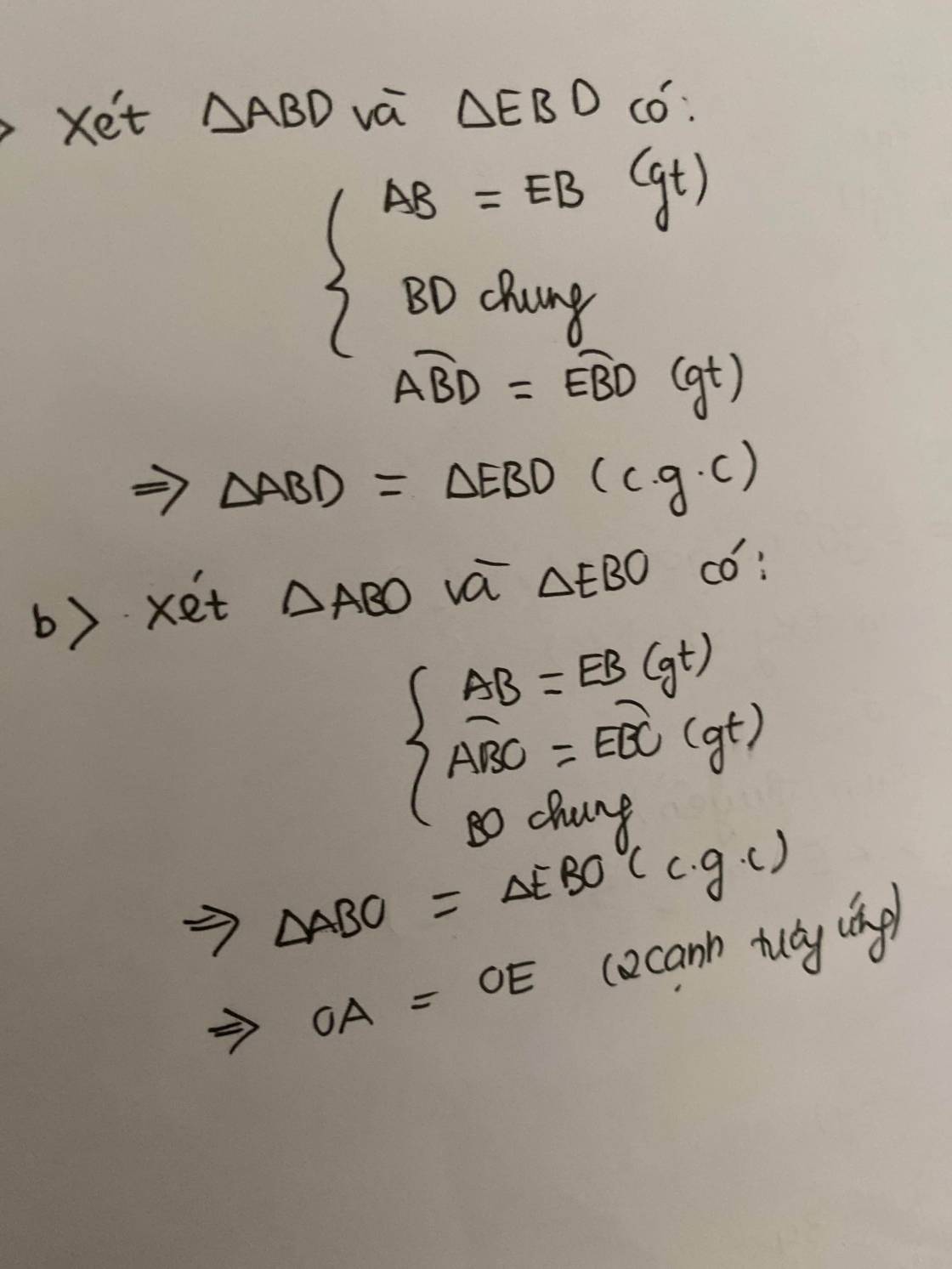
Bạn làm được bài này chưa vậy giúp mình
a) Xét tam giác ABD và tam giác EBD có :
AB= BE ( giả thiết ) (1)
Góc B1 = góc B2 ( vì tia BD là tia phân giác ) (2)
BD : cạnh chung (3)
Từ (1) ;(2) và (3) => tam giác ABD = tam giác EBD ( cạnh - góc - cạnh )
b) Vì tam giác ABD = tam giác EBD ( chứng minh ở câu a)
=> góc BAD = góc BED ( cặp góc tương ứng )
Mà góc BAD = 90 độ
=> BED = 90 độ
c) Vì góc BED = 90 độ
=> tam giác BED vuông
d) Vì AH vuông góc với BC ( giả thiết) (1)
và DE vuông góc với BC ( giả thiết ) (2)
Từ (1) và (2) => AH // DE ( điều phải chứng minh).