Giải pt
giúp mình câu d ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 9 2021
\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
12 tháng 6 2021
\(x^4+3x^2=0\)
Có \(x^4\ge0;\forall x\); \(3x^2\ge0;\forall x\)
=> VT\(\ge0;\forall x\)
Dấu = xảy ra <=> x=0
Ý C
LT
0
6 tháng 3 2023
=>(50x+50x+250+65x+11050)*1,1=216500
=>165x+11300=196818,1818
=>165x=185518,1818
=>\(x\simeq124.353\)
25 tháng 6 2023
c: ĐKXĐ: x<>8
\(\dfrac{3}{2x-16}+\dfrac{3x-20}{x-8}+\dfrac{1}{8}=\dfrac{13x-102}{3x-24}\)
=>\(\dfrac{9}{6\left(x-8\right)}+\dfrac{18x-120}{6\left(x-8\right)}-\dfrac{26x-204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{18x-111-26x+204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{-8x+93}{6x-48}=\dfrac{-1}{8}\)
=>\(\dfrac{8x-93}{6x-48}=\dfrac{1}{8}\)
=>8(8x-93)=6x-48
=>64x-744-6x+48=0
=>58x=696
=>x=12
d: ĐKXĐ: x<>1; x<>-1
\(\dfrac{6}{x^2-1}+5=\dfrac{8x-1}{4x+4}+\dfrac{12x-1}{4x-4}\)
=>\(\dfrac{24}{4\left(x-1\right)\left(x+1\right)}+\dfrac{20\left(x^2-1\right)}{4\left(x-1\right)\left(x+1\right)}=\dfrac{\left(8x-1\right)\left(x-1\right)+\left(12x-1\right)\left(x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
=>8x^2-9x+1+12x^2+12x-x-1=24+20x^2-20
=>20x^2+2x=20x^2+4
=>2x=4
=>x=2(loại)
TP
Thảo Phương
CTVVIP
26 tháng 7 2021
a) Gọi x, y lần lượt là số mol Al, Fe
2Al + 3H2SO4 → Al2(SO4)3 + 3H2
Fe + H2SO4 → FeSO4+ H2
\(\left\{{}\begin{matrix}27x+56y=5,54\\\dfrac{3}{2}x+y=\dfrac{3,584}{22,4}\end{matrix}\right.\)
=> x=0,06 , y =0,07
=> \(m_{Al}=1,62\left(g\right);m_{Fe}=3,92\left(g\right)\)
b) \(n_{H_2SO_4\left(pứ\right)}=n_{H_2}=0,16\left(mol\right)\)
=> \(m_{H_2SO_4\left(pứ\right)}=0,16.98=15,68\left(g\right)\)
c) \(m_{ddH_2SO_4}=\dfrac{15,68}{20\%}=78,4\left(g\right)\)
c) 2NaOH + H2SO4 → Na2SO4 + 2H2O
\(n_{H_2SO_4\left(dư\right)}=\dfrac{1}{2}n_{NaOH}=\dfrac{1}{2}.0,25.0,6=0,075\left(mol\right)\)
=> \(m_{H_2SO_4\left(bđ\right)}=15,68+0,075.98=23,03\left(g\right)\)
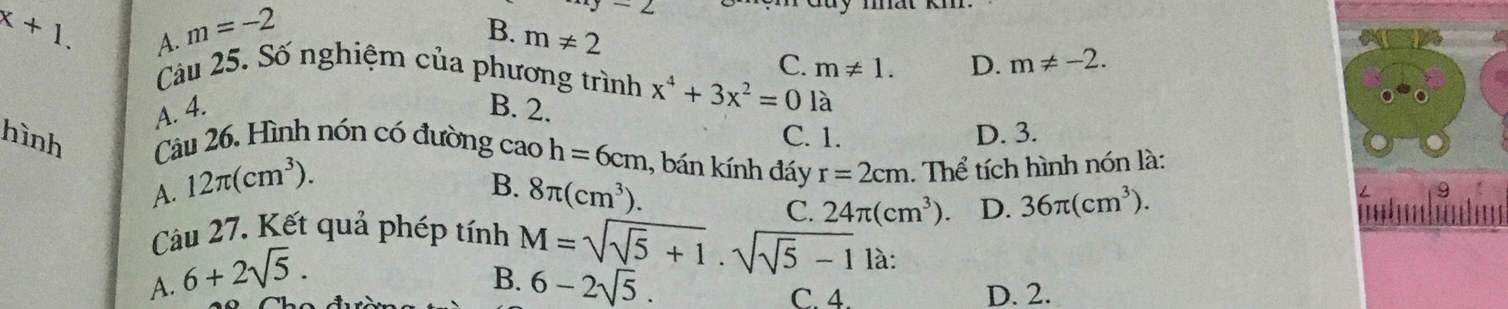
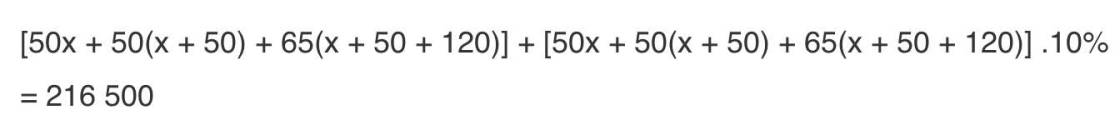
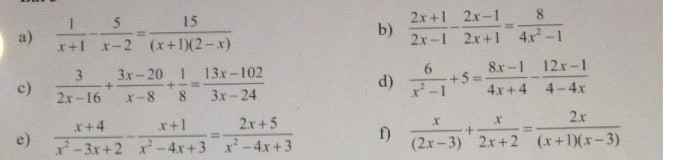
\(\dfrac{x-4}{x-1}+\dfrac{x+4}{x+1}=2\)
ĐKXĐ: \(x\ne\pm1\)
\(\Leftrightarrow\dfrac{\left(x-4\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{\left(x+4\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{2\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow x^2-3x-4+x^2+3x-4=2\left(x^2-1\right)\)
\(\Leftrightarrow2x^2-8-2x^2+2=0\)
\(\Leftrightarrow-6=0\) (Vô lí)
Vậy phương trình trên vô nghiệm.