Cho tam giác ABC nhọn các đường cao BD và CE cắt nhau tại H . chứng minh
a) AE. AB=AD. AC
b) tam giác ABE đồng dạng tam giác ACB
c) AH/AM+BH/BD+CH/CR = 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2022
1: Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{A}\) chung
Do đó: ΔABD∼ΔACE
Suy ra: AB/AC=AD/AE
hay \(AB\cdot AE=AC\cdot AD\)
2: Xét ΔADE và ΔABC có
AD/AB=AE/AC
\(\widehat{DAE}\) chung
Do đó:ΔADE∼ΔABC
20 tháng 4 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E co
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE;AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
24 tháng 4 2017
Khó king khủng em mới học lớp 4 thôi để em ăn cháo sen bát bảo minh trung làm được ngay nhưng phải làm thêm tí bò húc với lại rượu đế ! la la la la la ta là một con người
9 tháng 5 2023
a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE; AD/AB=AE/AC
c: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
=>góc AED=góc ACB
24 tháng 3 2023
Xét \(\Delta AEC\&\Delta ADB\\ \) có:
\(\widehat{A}=\widehat{A}\\ \widehat{E}=\widehat{D}=90^o\\ \Rightarrow\Delta AEC\sim\Delta ADB\left(đpcm\right)\)
b) vì\(\Delta AEC\sim\Delta ADB\Leftrightarrow\dfrac{AB}{AE}=\dfrac{AC}{AD}\Leftrightarrow\dfrac{3}{AE}=\dfrac{5}{2}\Rightarrow AE=\dfrac{3\cdot2}{5}=1.2cm\)
KV
24 tháng 3 2023
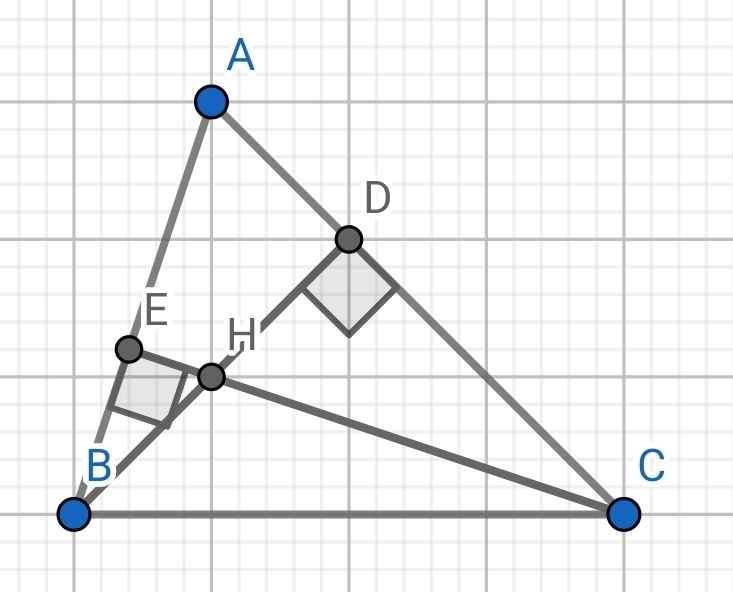
a) Xét ∆ADB và ∆ACE có:
∠ADB = ∠ACE = 90⁰
∠A chung
⇒ ∆ADB ∽ ∆ACE (g-g)
b) Do ∆ADB ∽ ∆ACE (cmt)
⇒ AD/AC = AB/AE
⇒ AE = AB.AC/AD
= 2.3/5
= 1,2 (cm)
Cái cuối là bằng 2 nha mn mik cần gấp mong mn giúp
a)xét tam giác ADB và tam giác AEC
chung A
E=D=90
=>ADB đồng dạng vs aAEC(gg)
=>AE.AB=AD.AC
b)xét 2 tam giác có
AE/AC=AD/AB
chung A
=>ABE đồng dạng với ACB
kb ko bn