Viết thuật toán giải phương trình bậc 2
ax2+bx+c=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
13 tháng 3 2021
Bài 1:
Thuật toán:
B1: Nhập a,b,c
B2: Tính \(\Delta\) = b2-4ac;
B3: Kiểm tra nếu \(\Delta\) >0 phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}\text{ }}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)
B4: Kiểm tra nếu \(\Delta\)<0 thì phương trình vô nghiệm
B5: Kiểm tra nếu \(\Delta\)=0 phương trình có 2 nghiệm kép \(x_1=x_2=-\dfrac{b}{2a}\)
Viết chương trình:
Program HOC24;
var a,b,c: integer;
x1,x2: real;
denta: longint;
begin
write('Nhap a; b; c: '); readln(a,b,c);
denta:=b*b-4*a*c;
if denta>0 then
begin
write('x1= ',(-b+sqrt(denta))/(2*a):1:2);
write('x2= ',(-b-sqrt(denta))/(2*a):1:2);
end;
if denta<0 then write('Phuong trinh vo nghiem');
if denta=0 then write('x= ',-b/2*a:1:2);
readln
end.
ML
13 tháng 3 2021
Bài 2:
Thuật toán:
B1: Nhập a,b
B2: Kiểm tra nếu a=0 và b=0 thì phương trình có vô số nghiệm
B3: Kiểm tra nếu a=0 thì phương trình vô nghiệm
B4: Kiểm tra nếu a khác 0 thì có nghiệm x=-b/a;
Viết chương trình:
Program HOC24;
var a,b: integer;
x: real;
begin
write('Nhap a; b: '); readln(a,b);
if a=0 and b=0 then write('Phuong trinh co vo so nghiem');
if a=0 then write('Phuong trinh vo nghiem');
if a<>0 then write('x=',-b/a:1:2);
readln
end.
NC
1
11 tháng 5 2017
Thuật toán giải phương trình bậc nhất:
Bước 1: Nhập a, b;
Bước 2: Nếu a = 0, B≠ 0 thì thông báo vô nghiệm rồi kết thúc;
Bước 3: Nếu a = 0, B = 0 thì thông báo phương trình nghiệm đúng với mọi giá trị rồi kết thúc;
Bước 4: Nếu a ≠ 0 thì x = -b/a thông báo phương trinh có nghiệm duy nhất là x rồi kết thúc
TT
1
16 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
NT
0
PN
1
Y
4 tháng 1 2022
Tham khảo:
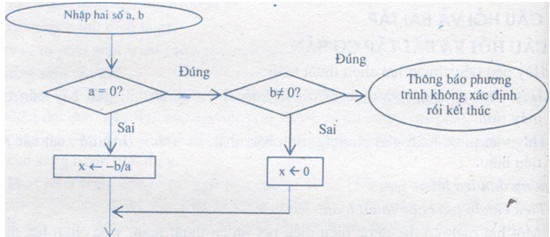
Thuật toán giải phương trình ax + b = 0
- Bằng liệt kê tuần tự
Bước 1: Nhập hai số thực a, b
Bước 2. Nếu a = 0
Bước 2.1. Nếu b ≠0 thì thông báo phương trình vô định, rồi kết thúc;
Bước 2.2. Nếu b = 0 thì gán x <- 0 rồi chuyển sang bước 4;
Bước 3: x <- -b/a
Bước 4. Đưa ra nghiệm X, rồi kết thúc.
- Sơ đồ khối:
Đề xuất các test tiêu chuẩn
Để xét tất cả các trường hợp có thể xảy ra, ta sử dụng ba bộ test như sau:
i) a = 0, b = 1 (kiểm tra trường hợp phương trình vô định);
ii) a = 0,b = 0 (kiểm tra trường hợp nghiệm x=0);
iii) a = 3, b = 6 (kiểm tra trường hợp nghiêm , y = -b/a)
B1:nhập a,b,c
B2: Tính đen ta = b^2-4ac
B3: nếu a<0 thì phương trình vô nghiệm =>B6
B4:nếu a=0 thì pt có nghiệm kép x=-b/2a => B6
B5:nếu a>0 thì pt có 2 nghiệm phân biệt x1= (-b+căn đen ta)/2a ; x2= (-b-căn đen ta)/2a =>B6
B6 :kết thúc,
nếu muốn vẽ bằng sơ đồ khối thì xem tại: https://vubinh94.wordpress.com/tag/so-do-khoi-giai-phuong-trinh-bac-2-ax2bxc0/