Cho hàm số y=f(x) có đạo hàm trên R và thỏa mãn f(1+3x)=2x-f(1-2x) với mọi \(x\in R\) . Lập phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=1 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 8 2017
Đáp án A
Với x=0 thay vào hai vế của đẳng thức f 2 1 + 2 x = x − f 3 1 − x ta có f 2 1 = − f 3 1 .
Đạo hàm hai vế của đẳng thức đã cho, ta có:
4 f 1 + 2 x . f ' 1 + 2 x = 1 + 3 f 2 1 − x . f ' 1 − x → x = 0 2 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1
Ta có hệ phương trình sau: f 2 1 = − f 3 1 4 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1
⇔ f 2 1 f 1 + 1 = 0 4 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1 ⇔ f 1 = − 1 f ' 1 = − 1 7
Vậy tiếp tuyến cần tìm là
y
=
f
'
1
.
x
−
1
+
f
1
=
−
1
7
x
−
1
−
1
⇔
y
=
−
1
7
x
−
6
7
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2021
Thay \(x=1\Rightarrow2f\left(2\right)+3f\left(2\right)=10\Rightarrow f\left(2\right)=5\)
Đạo hàm 2 vế giả thiết:
\(-6f'\left(5-3x\right)+3f'\left(x+1\right)=2x+4\)
Thay \(x=1\)
\(-6f'\left(2\right)+3f'\left(2\right)=6\Rightarrow f'\left(2\right)=-2\)
Phương trình tiếp tuyến:
\(y=-2\left(x-2\right)+5=-2x+9\)
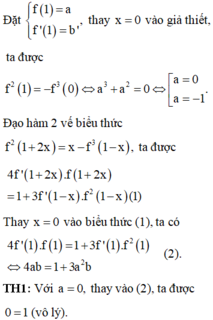
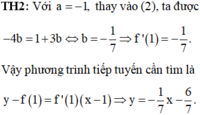
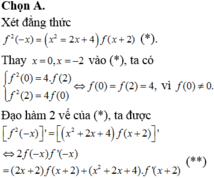
Lời giải:
Từ $f(1+3x)=2x-f(1-2x)$ thay $x=0$ suy ra $f(1)=1$
$f(1+3x)=2x-f(1-2x)$
$\Rightarrow f'(1+3x)=(2x)'-f'(1-2x)$
$\Leftrightarrow 3f'(1+3x)=2+2f'(1-2x)$. Thay $x=0$ suy ra $f'(1)=2$
PTTT của $f(x)$ tại điểm $x=1$ là:
$y=f'(1)(x-1)+f(1)=2(x-1)+1=2x-1$
cho em hỏi là sao lại thay x=0 mà không phải số khác ạ?