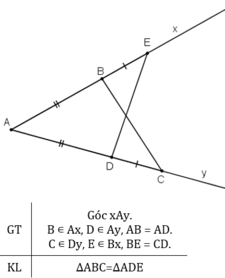
Cho góc xAy. Lấy điểm B trên tia Ax, điểm D trên tia Ay sao cho AB = AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh rằng tam giác ABC bằng tam giác ADE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 2 2018
Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.
Xét ΔABC và Δ ADE có:
AC = AE (cmt)
Góc A chung
AB = AD (gt)
⇒ ΔABC = ΔADE (c.g.c)
12 tháng 11 2016
Ta có hình vẽ:Xét tam giác ABC và tam giác ADE có
-góc A: góc chung
-AB = AD (GT)
-BE = DC (GT)
Vậy \(\Delta\)ABC = \(\Delta\)ADE (c.g.c)
27 tháng 11 2015
Tự vẽ hình
Xét tam giác ABC và tam giác ADE , ta có:
AB = AD (1) (gt)
EB = DC ; AB = AD => AB + BE = AD+DC nên AE = AC (2) (gt)
Góc A chung (3)
Từ (1) ; (2) ; (3) => \(\Delta ABC=\Delta ADE\)
16 tháng 10 2016
Điều kiện: xOy < 180o
Ta có hình vẽ:
Vì AB = AD (gt), BE = DC (gt)
=> AB + BE = AD + DC
hay AE = AC
Xét Δ ABC và Δ ADE có:
AC = AE (chứng minh trên)
A là góc chung
AB = AD (gt)
Do đó, Δ ABC = Δ ADE (c.g.c) (đpcm)
