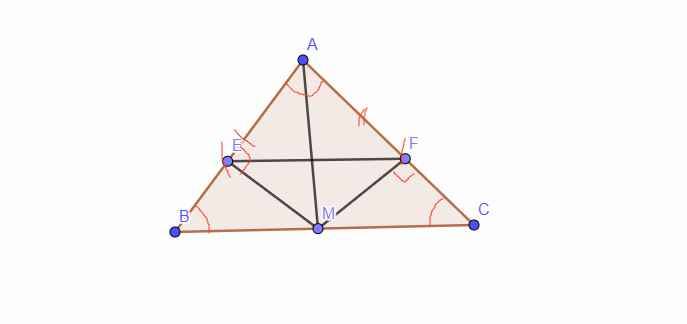
cho tam giác ABC cân tại A, M là trung điểm của BC. Từ M kẻ các đường thẳng ME song song AC, MF song song với AB. Chứng minh tứ giác BCFE là hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
18 tháng 11 2016
Xét ΔABC có MF // AB; BM=CM (gt)
=> AF=CF
Cmtt, ta đc: AE=BE
Do đó EF là đường TB ΔABC
=> EF // BC
Nên BCFE là hình thang (1)
Lại có: ΔABC cân tại A
=> B = C (2)
Từ (1)(2) suy ra BCFE là hình thang cân.
Hình vẽ ko đẹp lắm +_+ thông cảm hen----cx có nhiều cách giải khác nx nha bn
14 tháng 8 2021
a: Xét tứ giác BMEC có ME//BC
nên BMEC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMEC là hình thang cân
b: Xét ΔABC có
M là trung điểm của AB
ME//BC
Do đó: E là trung điểm của AC
Xét ΔABC có
M là trung điểm của AB
MF//AC
Do đó: F là trung điểm của BC
Xét ΔABC có
M là trung điểm của AB
F là trung điểm của BC
Do đó: MF là đường trung bình của ΔBAC
Suy ra: \(MF=\dfrac{AC}{2}\)
mà \(EC=\dfrac{AC}{2}\)
nên MF=EC
Xét tứ giác MECF có
MF//EC
MF=EC
Do đó: MECF là hình bình hành
14 tháng 8 2021
c: Xét ΔABC có
M là trung điểm của AB
E là trung điểm của AC
Do đó: ME là đường trung bình của ΔABC
Suy ra: ME//BC và \(ME=\dfrac{BC}{2}\)
mà \(BF=\dfrac{BC}{2}\)
nên ME//BF và ME=BF
Xét tứ giác MEFB có
ME//BF
ME=BF
Do đó: MEFB là hình bình hành
Suy ra: Hai đường chéo MF và BE cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của MF
nên I là trung điểm của BE
hay B,I,E thẳng hàng
1 tháng 12 2016
Bài 1 : Ta có MB = MC ( gt) , ME // AC => E là trung điểm của AB ( đường thẳng qua trung điểm cạnh tam giác . . )
MB = MC ( gt) , MF // AB ⇒ F là trung điểm của AC ( đường thẳng qua trung điểm cạnh tam giác . . . )
⇒ EF là đường trung bình của tam giác ABC . ⇒ EF // BC Vậy tứ giác BCEF là hình thang
. Mặt khác góc B = góc C ( tam giác ABC cân – gt) ⇒ Tứ giác BCEF là hình thang cân.
Bài 2: a/ chứng minh tứ giác có 2 cặp cạnh đối song song ( gt) nên AEGF là hình bình hành.
tứ giác có góc A = 900 ( gt)
Vậy AEGF là hình chữ nhật
b/ vì GF // AB ⇒ FI // EB
EI // BF (gt) ⇒ BEIF là hình bình hành ( 2 cặp cạnh đối // )
c/ Vì AF = FC , GB = GC ( gt) ⇒ GF là đường trung bình của tam giác ABC ⇒ GF = BE = 1/2 AB ⇒ GF = FI ( vì FI = BE do BEIF là hình bình hành)
⇒ GF // AB mà AB ⊥ AC ⇒ GI ⊥ AC tại F
Vậy AGCI là hình thoi ( hai đ/chéo vuông góc tại trung điểm mỗi đường )
d/ Để AGCI là hình vuông thì AC = GI . mà GI = 2GF = 2 EB = AB Vậy AGCI là hình vuông thì AC = AB ⇒ Tam giác ABC vuông cân tại A.
14 tháng 12 2018
Bài 2.
-Hình bn tự vẽ nhé!
Bài làm:
a, Có F là trung điểm của AC (gt)
\(\Rightarrow\)AF=\(\dfrac{1}{2}\)AC (1)
Xét tam giác ABC ta có:
E là trung điểm của AB (gt)
G là trung điểm của BC (gt)
\(\Rightarrow\)EG là đường trung bình của tam giác ABC
\(\Rightarrow\)EG=\(\dfrac{1}{2}\)AC và EG song song với AC hay EG song song với AF (2)
Từ (1) và (2)\(\Rightarrow\)AEGF là hình bình hành.
mà góc A= 90 độ (gt)\(\Rightarrow\)AEGF là hình chữ nhật.
AEGF là hcn nên có AE song song với GF ( Tính chất hcn) hay EB song song với IF (3)
mà EI song song với BF (gt) (4)
Từ (3) và (4)\(\Rightarrow\)BFIE là hình bình hành.
b, Theo a, ta có: BFIE là hình bình hành nên BE=FI (tính chất hình bình hành) và AEGF là hình chữ nhật nên AE=GF (tính chất hình chữ nhật)
mà AE=EB (E là trung điểm của AB)
\(\Rightarrow\)GF=FI.
Xét tứ giác AGCI có: FA=FC (F là trung điểm của AC), GF=FI (cmt)
\(\Rightarrow\)AGCI là hình bình hành.
mà GI vuông góc với AC nên hình bình hành AGCI là hình thoi
c, Theo b, ta có: AGCI là hình thoi
Để tứ giác (hình thoi) AGCI là hình vuông thì góc AGC= 90 độ hay AG vuông góc với BC.
Khi đó AG là đường cao của tam giác ABC
Mặt khác AC là đường trung tuyến của tam giác ABC ( G lf trung điểm của BC)\(\Rightarrow\) Tam giác ABC cân tại A
mà tam giác ABC vuông tại (gt) nên tam giác ABC vuông cân tại A thì AGCI là hình vuông.
5 tháng 3 2022
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành
9 tháng 1 2023
a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
9 tháng 1 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
Xét \(\Delta BCA:\)M là trung điểm BC ; \(ME\text{//}BC\left(E\in AB\right)\)
\(\Rightarrow ME\)là đường trung bình \(\Delta BCA\)
\(\Rightarrow E\) là trung điểm AB
Chứng minh tương tự được \(F\)là trung điểm AC
\(\Rightarrow EF\)là đường trung bình \(\Delta ABC\)
\(\Rightarrow EF\text{//}BC\)
Do đó BCFE là hình thang có \(\widehat{B}=\widehat{C}\)( \(\Delta ABC\)cân tại A) là 2 góc kề đáy BC bằng nhau nên là hình thang cân.
Vậy ...