có thể lập được bao nhiêu số có 3 chữ số khác nhau từ các số 0,1,2,3 sao cho mỗi số lập được đều chia hết cho 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 1 2017
Chọn C
Giả sử số lập được có dạng 
Ta có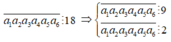 
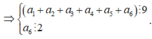
Vì 
nên ta có các trường hợp sau
Trường hợp 1:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+ Có 3 cách chọn chọn a 6
+ Có 5! cách chọn chọn bộ 5 số 
Suy ra có 3.5! = 360 số.
Trường hợp 2:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+
a
6
= 0, có 5! cách chọn bộ 5 số 
+
a
6
≠
0 khi đó
a
6
có 3 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số 
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+
a
6
= 0, có 5! cách chọn bộ 5 số 
+
a
6
≠
0 khi đó
a
6
có 1 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số 
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.
5 tháng 2 2018
Có thể lập được bao nhiêu số có 4 chữ số khác nhau từ các chữ số trên sao cho số vừa lập được chia hết cho 2 và 5 là 2350 ; 2530 ; 3250 ; 3520 ; 5230 ; 5320
30 tháng 7 2017
- Có 3 cách chon chữ số hàng trăm
- Có 3 cách chọn chữ số hàng chục
- Có 2 cách chọn chữu số hàng đơn vị
=> Từ các số đã cho ta lập được :
3 x 3 x 2 = 18 ( số )
bn tự liệt kê ra rồi sem số nào chia hết cho 9 thì viết ra
CM
13 tháng 1 2019
a. Lập số có 3 chữ số thì chữ số hàng trăm phải khác 0, nên chữ số hàng trăm có 3 cách chọn (3,5,6). Hàng chục có 3 cách chọn, hàng đơn vị có 2 cách chọn.
Vậy số các số phải tìm là: 3 x 3 x 2 = 18 (số)
b. Trong các số trên các số chia hết cho 9 là: 306, 360, 603, 630.
AH
Akai Haruma
Giáo viên
23 tháng 8 2021
Lời giải:
Gọi số thỏa mãn có dạng $\overline{a_1a_2a_3}$
Để số trên chia hết cho $3$ thì $a_1+a_2+a_3\vdots 3$
Thấy $3\leq a_1+a_2+a_3\leq 12$ nên $a_1+a_2+a_3\in \left\{3;6;9;12\right\}$
+) Để $a_1+a_2+a_3=3$ thì $(a_1,a_2,a_3)=(0,1,2)$
Ta lập được $2.2.1=4$ số thỏa mãn
+) Để $a_1+a_2+a_3=6$ thì $(a_1,a_2,a_3)=(0,1,5); (0,2,4); (1,2,3)$
Ta lập được $2.2.1+2.2.1+3.2.1=14$ số thỏa mãn
+) Để $a_1+a_2+a_3=9$ thì $(a_1,a_2,a_3)=(0,4,5); (1,3,5); (2,3,4)$
Ta lập được: $2.2.1+3.2.1+3.2.1=16$ số thỏa mãn
+) Để $a_1+a_2+a_3=12$ thì $(a_1,a_2,a_3)=(3,4,5)$
Ta lập được: $3.2.1=6$ số
Tóm lại lập được: $4+14+16+6=40$ số.
Các số đó là :
123,132,120,102,201,210,231,213,321,312
Vậy có 10 số
6 số : 123,132,213,231,321,312