BÀI 1: Cho ∆ABC nhọn. Vẽ về phía ngoài ∆ABC các ∆ đều ABD và ACE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:a) ∆ABE = ∆ADC b) Góc BMC = 120oBài 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).a) Chứng minh: EM + HC = NH.b) Chứng minh: EN // FM.Bài 3:Cho...
Đọc tiếp
BÀI 1: Cho ∆ABC nhọn. Vẽ về phía ngoài ∆ABC các ∆ đều ABD và ACE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:
a) ∆ABE = ∆ADC b) Góc BMC = 120o
Bài 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).
a) Chứng minh: EM + HC = NH.
b) Chứng minh: EN // FM.
Bài 3:Cho cạnh hình vuông ABCD có độ dài là 1. Trên các cạnh AB, AD lấy các điểm P, Q sao cho chu vi DAPQ bằng 2.
Chứng minh rằng : Góc PCQ = 45o
Bài 4:Cho tam giác vuông cân ABC (AB = AC), tia phân giác của các góc B và C cắt AC và AB lần lượt tại E và D.
a) Chứng minh rằng: BE = CD; AD = AE.
b) Gọi I là giao điểm của BE và CD. AI cắt BC ở M, chứng minh rằng các ∆MAB; MAC là tam giác vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE, các đường thẳng này cắt BC lần lượt ở K và H. Chứng minh rằng KH = KC.
Bài 5: Cho tam giác cân ABC (AB = AC ). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N. Chứng minh rằng:
a) DM = EN
b) Đường thẳng BC cắt MN tại trung điểm I của MN.
c) Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.

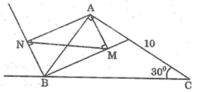

a. Trong tam giác vuông ABC, ta có :
\(AB=BC.\sin\widehat{C}=10.\sin30^o=10.\frac{1}{2}=5\left(cm\right)\)
\(AC=BC.\cos\widehat{C}=10.\cos30^o=10.\frac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
b)
Ta có : \(BM\perp BN\)( tính chất 2 góc kề bù ) \(\Rightarrow\widehat{MBN}=90^o\left(1\right)\)
\(AM\perp BM\left(gt\right)\Rightarrow\widehat{AMB}=90^o\left(2\right)\)
\(AN\perp BN\left(gt\right)\Rightarrow\widehat{ANB}=90^o\left(3\right)\)
Từ (1) (2) và (3) , suy ra : tứ giác AMBN là hình chữ nhật
\(\Rightarrow\Delta AMB=\Delta NBM\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{NMB}\)
Mà \(\widehat{ABM}=\widehat{MBC}\left(gt\right)\)
\(\Rightarrow\widehat{NMB}=\widehat{NBC}\)
Suy ra: MN // BC (có cặp góc so le trong bằng nhau)
Vì AMBN là hình chữ nhật nên AB = MN
)): gửi cả câu c) rồi mà cuối cùng lại 0 có , làm lại câu c) sang bên này :>
c)
Tam giác ABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
\(\Rightarrow\widehat{B}=90^o-\widehat{C}=90^o-30^o=60^o\)
\(\Rightarrow\widehat{ABM}=\frac{1}{2}\widehat{B}=\frac{1}{2}.60^o=30^o\)
Xét 2 tam giác ABC và MAB ,, ta có :
\(\widehat{BAC}=\widehat{AMB}=90^o\)
\(\widehat{ACB}=\widehat{ABM}=90^o\)
\(\Rightarrow\Delta ABC~\Delta MAB\left(g.g\right)\)
=> Tỉ số đồng dạnh \(k=\frac{AB}{BC}=\frac{5}{10}=\frac{1}{2}\)