Cho các số thực x,y phân biệt thỏa mãn x3+y3+12xy=64
Tính giá trị x+y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1
2
Những câu hỏi liên quan
12 tháng 1 2023
a: (x+y+z)^3-x^3-y^3-z^3
=(x+y+z-x)(x^2+2xy+y^2-x^2-xy-xz+z^2)-(y+z)(y^2-yz+z^2)
=(x+y)(y+z)(x+z)
b: x^3+y^3+z^3=1
x+y+z=1
=>x+y=1-z
x^3+y^3+z^3=1
=>(x+y)^3+z^3-3xy(x+y)=1
=>(1-z)^3+z^3-3xy(1-z)=1
=>1-3z-3z^2-z^3+z^3-3xy(1-z)=1
=>1-3z+3z^2-3xy(1-z)=1
=>-3z+3z^2-3xy(1-z)=0
=>-3z(1-z)-3xy(1-z)=0
=>(z-1)(z+xy)=0
=>z=1 và xy=0
=>z=1 và x=0; y=0
A=1+0+0=1
CM
16 tháng 2 2018
áp án B
Ta có: log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 ⇔ y + 1 log 3 x + 1 y + 1 + x − 1 y + 1 = 9
⇔ y + 1 log 3 c + 1 y + 1 + x + 1 y + 1 − 2 y = 11
⇔ y + 1 log 3 c + 1 y + 1 − 2 = 9 − x + 1 y + 1 *
Nếu x + 1 y + 1 > 9 ⇒ V T * > 0 ; V P * < 0
Ngược lại nếu x + 1 y + 1 < 9 ⇒ V T * < 0 ; V P * > 0
Do đó * ⇔ x + 1 y + 1 = 9 ⇔ x y + x + y = 8
Khi đó P = x + y 3 − 3 x y x + y − 57 x + y = x + y 3 − 3 8 − x − y x + y − 57 x + y
Đặt t = x + y ≥ 2 ⇒ f t = t 3 − 3 8 − t t − 57 t = t 3 + 3 t 2 − 81 t
⇒ f ' t = 3 t 2 + 6 t − 81 = 0 ⇒ t = − 1 + 2 7 ⇒ P min = f − 1 + 2 7 = 83 − 112 7 ⇒ a + b = − 29
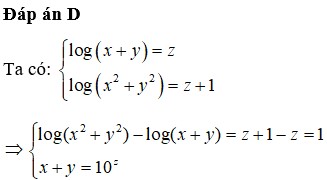
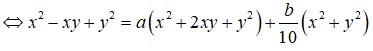
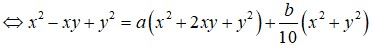
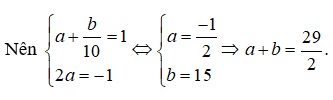
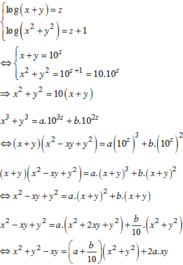
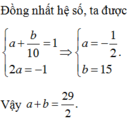
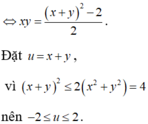
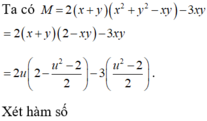
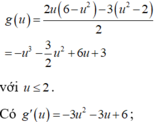
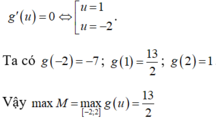
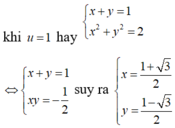
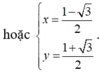
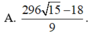
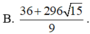
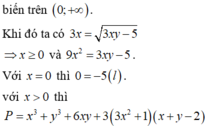
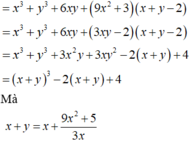
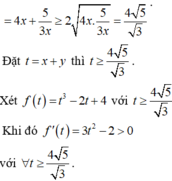
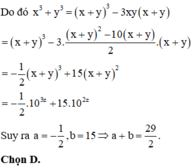
Ta có: x3 + y3 + 3xy(x+y) = (x+y)3(1)
Mà x3 + y3 + 12xy = 64 (2)
Trừ vé với vế của (1) và (2), ta được:
3xy(x+y) - 12xy = (x+y)3 - 64
<=> 3xy(x + y - 4) = (x + y - 4)[(x + y)2 + 4(x +y) + 16)
<=> 3xy(x + y - 4) = (x + y - 4)(x2 + 2xy + y2 + 4x + 4y + 16)
<=> (x + y - 4)(x2 - xy + y2 + 4x + 4y + 16) = 0
<=> \(\left[{}\begin{matrix}x+y-4=0\\x^2-xy+y^2+4x+4y+16=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x+y=4\left(1\right)\\4x^2-4xy+4y^2+16x+16y+64=0\left(2\right)\end{matrix}\right.\)
Ta thấy:
(2) <=>\(4x^2-4xy+y^2+8\left(2x+y\right)+16+3y^2+8y+48=0\)
<=> \(\left(2x-y+4\right)^2+2y^2+8y+8+y^2+40=0\)
<=> \(\left(2x-y+4\right)^2+2\left(y+2\right)^2+y^2+40=0\)
Vì \(\left(2x-y+4\right)^2;2\left(y+2\right)^2;y^2\ge0,\forall x,y\) (rõ như ban ngày)
=> \(\left(2x-y+4\right)^2+2\left(y+2\right)^2+y^2+40\ge40>0\)
=> Biểu thức (2) không có số thực x, y thỏa mãn. => Không tìm được x + y
Vậy x + y = 4.
\(x^3++y^3+12xy=64\) (1)
\(\left(1\right)\Leftrightarrow x^3+y^3+\left(-4\right)^3-3xy\left(-4\right)=0\)
áp dụng
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)\)
\(\left(1\right)\Leftrightarrow\left[x+y+\left(-4\right)\right]\left[x^2+y^2+\left(-4\right)^2-xy-y\left(-4\right)-x\left(-4\right)\right]=0\)
\(\Leftrightarrow\left(x+y-4\right)\left(x^2+y^2+16-xy+4y+4x\right)=0\) (2)
Xét \(x^2+y^2+16-xy+4y+4x=\)
\(=x^2-\left(y-4\right)x+y^2+4y+16\)
\(\Delta=\left(y-4\right)^2-4\left(y^2+4y+16\right)=\)
\(=y^2-8y+16-4y^2-16y-64=\)
\(-3y^2-24y-48\)
\(\Delta\) có
\(\delta=24^2-4.3.48=0\)
\(a=-3< 0\)
\(\Rightarrow\Delta< 0\forall y\)
\(\Rightarrow x^2-\left(y-4\right)x+y^2+4y+16\) có
\(\Delta< 0;a-1>0\)
\(\Rightarrow x^2-\left(y-4\right)x+y^2+4y+16>0\forall x\)
\(\Rightarrow\left(2\right)\Leftrightarrow x+y-4=0\Rightarrow x+y=4\)