giải ci tiết hộ e vs ạ
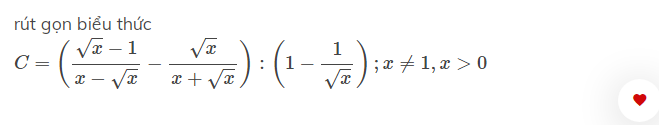
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{\sqrt{2}}{\sqrt{2}+1}+\dfrac{1}{3}\cdot3\sqrt{2}\)
\(=\sqrt{2}\left(\sqrt{2}-1\right)+\sqrt{2}=2\)

vì trên sân khấu có nhiều đèn nên ca sĩ khi biểu diễn thường mặc trang phục có nhiều học tiết trang trí để giúp cho dễ bắt sáng,nổi bật hơn

\(\Rightarrow\dfrac{R1}{R2}=\dfrac{\dfrac{p1.L}{S1}}{\dfrac{p2.L}{S2}}=1=\dfrac{p1.S2}{p2.S1}=\dfrac{1,7.10^{-8}\left(\dfrac{d}{2}\right)^2\pi}{1,1.10^{-6}.\left(\dfrac{d1}{2}\right)^2\pi}\)
\(\Rightarrow1=\dfrac{17\left(\dfrac{0,0001}{2}\right)^2}{1100\left(\dfrac{d1}{2}\right)^2}\Rightarrow d1=1,24.10^{-5}m\)

Đặt \(A=\dfrac{1}{\sqrt[3]{a+7b}}+\dfrac{1}{\sqrt[3]{b+7c}}+\dfrac{1}{\sqrt[3]{c+7a}}\)
\(A=\dfrac{\sqrt[3]{64}}{\sqrt[3]{8.8\left(a+7b\right)}}+\dfrac{\sqrt[3]{64}}{\sqrt[3]{8.8\left(b+7c\right)}}+\dfrac{\sqrt[3]{64}}{\sqrt[3]{8.8\left(c+7a\right)}}\)
\(\ge\dfrac{4}{\dfrac{8+8+a+7b}{3}}+\dfrac{4}{\dfrac{8+8+b+7c}{3}}+\dfrac{4}{\dfrac{8+8+c+7a}{3}}\ge\dfrac{\left(2+2+2\right)^2}{\dfrac{8+8+a+7b+8+8+b+7c+8+8+c+7a}{3}}\)
\(=\dfrac{36.3}{8\left(a+b+c\right)+48}=\dfrac{3}{2}\)
Vậy \(A_{min}=\dfrac{3}{2}\Leftrightarrow a=b=c=1\)



Số học sinh lớp 4A là 55x5/11=25(bạn)
Số học sinh lớp 4B là 55-25=30(bạn)
có số học sinh lớp 4A là
55x5/11=25(bạn)
có số học sinh lớp 4B là;
55-25=30(bạn)
\(C=\left(\dfrac{\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{\sqrt{x}}{x+\sqrt{x}}\right):\left(1-\dfrac{1}{\sqrt{x}}\right)\)
\(C=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\left(1-\dfrac{1}{\sqrt{x}}\right)\)
\(C=\left(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)-\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}}\right)\)
\(C=\dfrac{x-1-x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(C=\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(C=\dfrac{1}{x-1}\)