Biết phương trình: x2 + ax + bc = 0 và phương trình: x2 + bx + ac = 0 có 1 đúng nghiệm chung và \(a\ne b\ne c\) ; \(c\ne0\)
Chứng minh rằng: các nghiệm còn lại của hai phương trình trên là nghiệm của phương trình: x2 + cx + ab = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
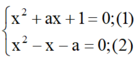
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
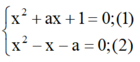
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.

Chọn đáp án B
Gọi x 0 là nghiệm thực chung của 2 phương trình
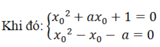
⇒ x 0 2 + a x 0 + 1 = x 0 2 - x 0 - a ⇔ (a + 1) x 0 = -(a + 1) ⇔ x 0 = -1
Thay x 0 = -1 vào phương trình x 0 2 + a x 0 + 1 = 0 tìm được a = 2


c và d là nghiệm của phương trình:
x 2 + a x + b ⇒ ⇒ c + d = − a ( 1 ) c d = b ( 2 )
a, b là nghiệm của phương trình:
x 2 + c x + d = 0 ⇒ ⇒ a + b = − c ( 3 ) a b = d ( 4 )

Đáp án cần chọn là: A
Gọi x0 là nghiệm chung của 2 phương trình
Ta có:\(x_0^2+ax_0+bc=0;x_0^2+bx_0+ca=0\)
\(\Rightarrow\left(a-b\right)x_0=c\left(a-b\right)\)
Mà \(a\ne b\Rightarrow x_0=c\)
Gọi các nghiệm của phương trình x2 +ax + bc = 0 và x2 + bx + ac = 0 là x1 và x2
Theo Viet ta có:\(x_0x_1=bc;x_0x_2=ca\)
Mà \(x_0=c\ne0\Rightarrow x_1=b;x_2=a\)
Do b;c là các nghiệm của phương trình x2 +ax + bc = 0 nên b+c=-a => -c=a+b => a,b là các nghiệm của phương trình:
x2 - ( a+b ) x + ab = 0 hay x2 + cx + ab = 0