Cho hình vuông ABCD. Gọi M,N là hai điểm lần lượt trên hai cạnh BC và CD sao cho góc MAN= 45 độ. Chứng minh chu vi tam giác CMN = 1/2 chu vi hình vuông ABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


https://www.slideshare.net/PhamNguyenThucLinh/hc-sinh-gii-hnh-hc-8

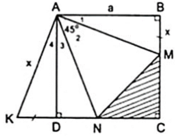
Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
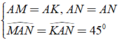 ⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.

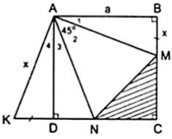
Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
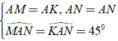 ⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.

Gọi chu vi tam giác CMN bằng p.
Tìm ý tưởng: p = BC + CD, hệ thức này gợi cho ta đến tính chất của đường tròn bàng tiếp (xem bài 2). Ở đây là đường tròn bàng tiếp góc C của ΔCMN.
Gọi B’, D’ lần lượt là các tiếp điểm của đường tròn bàng tiếp góc C của ΔCMN với đường kéo dài cạnh CM, CN.
Ta đã có, CB’ = CD’ = = CB = CD B’ B và D D’. Do đó, tâm đường tròn bàng tiếp góc C của tam giác CMN là điểm A.
Từ đó, .
Gọi chu vi tam giác CMN bằng p.
Tìm ý tưởng: p = BC + CD, hệ thức này gợi cho ta đến tính chất của đường tròn bàng tiếp (xem bài 2). Ở đây là đường tròn bàng tiếp góc C của ΔCMN.
Gọi B’, D’ lần lượt là các tiếp điểm của đường tròn bàng tiếp góc C của ΔCMN với đường kéo dài cạnh CM, CN.
Ta đã có, CB’ = CD’ = = CB = CD B’ B và D D’. Do đó, tâm đường tròn bàng tiếp góc C của tam giác CMN là điểm A.
Từ đó, .
Trên tia đối của tia DC lấy E sao cho DE=BM
Xét ΔABM vuông tại B và ΔADE vuông tại D có
AB=AD
BM=DE
=>ΔABM=ΔADE
=>AM=AE
góc BAM+góc MAN+góc NAD=góc BAD=90 độ
=>góc BAM+góc NAD=45 độ
=>góc EAN=45 độ
Xét ΔEAN và ΔMAN có
AE=AM
góc EAN=góc MAN
AN chung
=>ΔEAN=ΔMAN
=>EN=MN
C CMN=CM+MN+CN
=CM+MN+CN
=CM+ED+DN+CN
=CM+BM+DN+CN
=BC+CD=1/2*C ABCD