Cho một điểm $O$ nằm trên đường thẳng $x x'$. Trên nửa mặt phẳng có bờ là $x x'$ dựng hai tia $O M$ và $O N$ sao cho $\widehat{x O M}=\widehat{N O x'}=30^{\circ}$. Gọi tia $O t$ là phân giác của $\widehat{M O N}$. Chứng minh $O t \perp x x'$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
1 tháng 8 2019
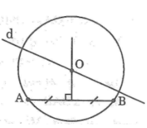
- Vì A và B là hai điểm nằm trên đường tròn tâm O nên OA = OB.
- Suy ra O thuộc đường trung trực của đoạn AB.
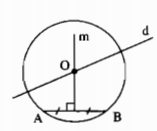
Vì tâm O nằm trên đường thẳng d nên O là giao điểm của đường trung trực của AB và đường thẳng d.
- Dựng đường thẳng m là đường trung trực của AB cắt d tại O.
- Vẽ đường tròn tâm O bán kính OA (hoặc OB).
* Lưu ý:
- Nếu m // d thì không dựng được tâm O
- Nếu m trùng với d thì có vô số điểm chung O do đó có vô số đường tròn thỏa mãn bài toán.

12 tháng 3 2021
bài 1. Góc KOM có độ là:
(80-20)/2=30 (độ)
Góc MOH có độ là:
30+20=50 (độ)
Vậy góc MOH=50 độ
KOM=30 độ
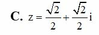

\(\widehat{MON}=\widehat{xOx'}-\widehat{xOM}-\widehat{NOx'}=180^o-30^o-30^o=120^o\)
\(\widehat{MOt}=\widehat{NOt}=\dfrac{\widehat{MON}}{2}=60^o\)
\(\Rightarrow\widehat{xOt}=\widehat{xOM}+\widehat{MOt}=30^o+60^o=90^o\Rightarrow ot\perp xx'\)
MON=xOx′−xOM−NOx′=180o−30o−30o=120o
\widehat{MOt}=\widehat{NOt}=\dfrac{\widehat{MON}}{2}=60^oMOt=NOt=2MON=60o
\Rightarrow\widehat{xOt}=\widehat{xOM}+\widehat{MOt}=30^o+60^o=90^o\Rightarrow ot\perp xx'⇒xOt=xOM+MOt=30o+60o=90o⇒ot⊥xx