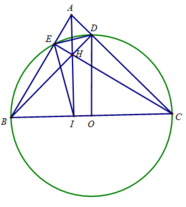
Cho tam giác ABC nhọn nội tiếp (O), có đường cao AH, gọi M,N lần lượt là hình chiếu của H trên AB,AC. MN cắt (O) tại D, cắt BC tại K. Gọi I là trung điểm AH, IK cắt AB, AC lần lượt tại E và F.
CM tứ giác BMCN nội tiếp
Tam giác ADH cân
I là trung điểm EF


a: ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
=>AM/AC=AN/AB
=>góc AMN=góc ACB
=>góc NMB+góc NCB=180 độ
=>NMBC nội tiếp
b: kẻ đường kính AL
góc ACL=90 độ
AC*AN=AH^2
ΔAIN đồng dạng với ΔACE
=>AI/AC=AN/AE
=>AI*AE=AH^2
góc ADE=90 độ
=>ΔADE vuông tại D
=>AI*AE=AD^2=AH^2
=>AD=AH