Câu 7(2 điểm): Từ điểm M ở ngoài đường tròn (O) v tilde e các tiếp tuyến MA, MB với (O). Vẽ đường kính AC, tiếp tuyến tại C của đường tròn (O) cắt AB ở D. Giao của MO và AB là I. Chứng minh răng: a) Tủ giác MAOB nội tiếp. b) Tích AB.ADkhông đổi khi M di chuyển.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2018
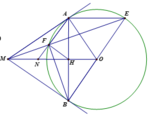
1) Chứng minh: Tứ giác MAOB nội tiếp một đường tròn
Vẽ được các yếu tố để chứng minh phần (1).
Ta có M B O ^ = 90 0 , M A O ^ = 90 0 (theo t/c của tiếp tuyến và bán kính)
Suy ra: M A O ^ + M B O ^ = 180 0 .Vậy tứ giác MAOB nội tiếp đường tròn.
2) Chứng minh: MN2 = NF. NA và MN = NH
Ta có A E / / M O ⇒ A E M ^ = E M N ^ mà A E M ^ = M A F ^ ⇒ E M N ^ = M A F ^
Δ N M F v à Δ N A M có: M N A ^ chung; E M N ^ = M A F ^
nên Δ N M F đồng dạng với Δ N A M
⇒ N M N F = N A N M ⇒ N M 2 = N F . N A 1
Mặt khác có: A B F ^ = A E F ^ ⇒ A B F ^ = E M N ^ h a y H B F ^ = F M H ^
=> MFHB là tứ giác nội tiếp
⇒ F H M ^ = F B M ^ = F A B ^ h a y F H N ^ = N A H ^
Xét Δ N H F & Δ N A H c ó A N H ^ c h u n g ; N H F ^ = N A H ^
=> Δ N M F đồng dạng Δ N A H ⇒ ⇒ N H N F = N A N H ⇒ N H 2 = N F . N A 2
Từ (1) và (2) ta có NH = HM
3) Chứng minh: H B 2 H F 2 − EF M F = 1 .
Xét Δ M AF và Δ M E A có: A M E ^ chung, M A F ^ = M E A ^
suy ra Δ M AF đồng dạng với Δ M E A
⇒ M E M A = M A M F = A E A F ⇒ M E M F = A E 2 A F 2 (3)
Vì MFHB là tứ giác nội tiếp ⇒ M F B ^ = M H B ^ = 90 0 ⇒ B F E ^ = 90 0 và A F H ^ = A H N ^ = 90 0 ⇒ A F E ^ = B F H ^
Δ A E F và Δ H B F có: E F A ^ = B F H ^ ; F E A ^ = F B A ^
suy ra Δ A E F ~ Δ H B F
⇒ A E A F = H B H F ⇒ A E 2 A F 2 = H B 2 H F 2 (4)
Từ (3) và (4) ta có M E M F = H B 2 H F 2 ⇔ M F + F E M F = H B 2 H F 2 ⇔ 1 + F E M F = H B 2 H F 2 ⇔ H B 2 H F 2 − F E M F = 1
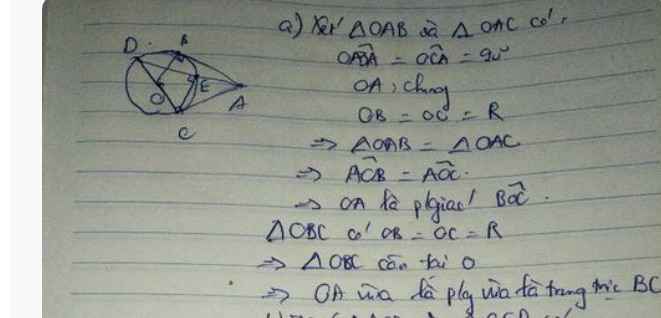
a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=180^0\)
nên MAOB là tứ giác nội tiếp
b: Xét (O) có
ΔABC nội tiếp
AC là đường kính
Do đó;ΔABC vuông tại B
Xét ΔACD vuông tại C có CB là đường cao
nên \(AB\cdot AD=AC^2=4R^2\)
Giải thích các bước giải:
a.Ta có: MA,MBMA,MB là tiếp tuyến của (O)→MO⊥AB(O)→MO⊥AB
Mà CDCD là tiếp tuyến của (O)→CD⊥AC(O)→CD⊥AC
→ˆOID=ˆOCD=90o→OID^=OCD^=90o
→O,I,D,C∈→O,I,D,C∈ đường tròn đường kính ODOD
b.Ta có: ˆAIO=ˆACD=90oAIO^=ACD^=90o
ˆOAI=ˆCADOAI^=CAD^
→ΔAIO∼ΔACD(g.g)→ΔAIO∼ΔACD(g.g)
→AIAC=AOAD→AIAC=AOAD
→AI.AD=AO.AC=R⋅2R=2R2=8→AI.AD=AO.AC=R⋅2R=2R2=8
→2AI.AD=16→2AI.AD=16
→AB.AD=16→AB.AD=16
Vì MA,MBMA,MB là tiếp tuyến của (O)→MO⊥AB=I(O)→MO⊥AB=I là trung điểm ABAB
→AB=2AI→AB=2AI
c.Gọi MC∩OD=EMC∩OD=E
Ta có:
ˆCAD=ˆOAI=90o−ˆIAM=ˆAMI=ˆAMOCAD^=OAI^=90o−IAM^=AMI^=AMO^
Vì CDCD là tiếp tuyến của (O)(O)
Mà ˆMAO=ˆDCA=90oMAO^=DCA^=90o
→ΔMAO∼ΔACD(g.g)→ΔMAO∼ΔACD(g.g)
→MAAC=AOCD→MAAC=AOCD
→MAAC=OCCD→MAAC=OCCD
→MACO=ACCD→MACO=ACCD
Mà ˆMAC=ˆOCD=90oMAC^=OCD^=90o
→ΔMAC∼ΔOCD(c.g.c)→ΔMAC∼ΔOCD(c.g.c)
→ˆCOD=ˆCMA→COD^=CMA^
→ˆCOE=ˆCMA→COE^=CMA^
Do ˆOCE=ˆACMOCE^=ACM^
→ΔCEO∼ΔCAM(g.g)→ΔCEO∼ΔCAM(g.g)
→ˆCEO=ˆCAM=90o→CEO^=CAM^=90o
→OD⊥MC