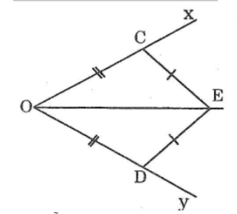
Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OD=OC. Vẽ các cung tròn tâm C và tâm D có cùng bán kính sao cho chúng cắt nhau ở điểm E nằm trong góc xOy. Chứng minh rằng OE là tia phân giác của góc xOy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 12 2017
Xét ΔCOE và ΔDOE. Ta có:
OE cạnh chung
OD = OC (giả thiết)
DE=CE ( bán kính 2 cung tròn có bán kính bằng nhau)
Suy ra: ΔCOE= ΔDOE(c.c.c)
Vậy : ∠(COE) =∠(DOE) (hai góc tương ứng)
Vì điểm E nằm trong góc xOy nên tia OE nằm giữa OC và OD (2)
Từ (1) và (2) suy ra: OE là tia phân giác của góc DOC hay OE là tia phân giác của góc xOy
23 tháng 11 2015
Cậu tự vẽ hình nha
Vì OD=OC
Vì bán kính tâm C và D cùng bán kính
suy ra DE=CE
Xét hai tam giác OCE và ODE
Ta có OD=OC
DE=CE
OE là cạnh chung
Vậy tam giác OCE bằng tam giác ODE
Suy ra góc COE bằng góc DOE
Vậy OE là tia phân giác của góc xoy
6 tháng 2 2023
a: Xét ΔOCE và ΔODE có
OC=OD
EC=ED
OE chung
=>ΔOCE=ΔODE
b: ΔOCE=ΔODE
=>góc COE=gócDOE
=>OE là phân giác của góc xOy
c: ΔOCE=ΔODE
=>góc OCE=góc ODE
H9
HT.Phong (9A5)
CTVHS
6 tháng 2 2023
Trong △COE và △DOE có
OE là cạnh chung
OC = OD (gt)
CE = DE (gt)
Do đó △COE = △DOE (c.c.c)
Suy ra \(\widehat{COE}\) = \(\widehat{DOE}\) (cặp góc tương ứng )
Vậy OE là tia phân giác của góc xOy
4 tháng 12 2021
a: Xét ΔAOC và ΔBOC có
OA=OB
OC chung
AC=BC
Do đó: ΔAOC=ΔBOC
4 tháng 12 2021
a: Xét ΔAOC và ΔBOC có
OA=OB
OC chung
AC=BC
Do đó: ΔAOC=ΔBOC
