Một ô tô đi từ A đến B cách nhau 60km trong một thời gian quy định. Trên nửa quảng đường đầu, ô tô đi với vận tốc kém vận tốc dự định mỗi giờ 6km. Trên nửa quãng đường sau, ô tô đi với vận tốc lớn hơn vận tốc dự định mỗi giờ 10km. Vì vậy, ô tô đến B đúng giờ quy định. Tính thời gian quy định để ô tô đi từ A đến B.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn xem lời giải tại đường link dưới nhé
Câu hỏi của Anh Aries - Toán lớp 8 - Học toán với OnlineMath

Tham khảo , nhưng bạn nhầm môn học rồi!
Gọi vận tốc dự định đi quãng đường AB = x km/giờ (x>0)
thời gian dự định đi quãng đường AB = 60/x
--> vận tốc đi nửa đường đầu (đi 30km đầu) = x + 10
thời gian đi nửa đường đầu = 30/(x + 10)
--> vận tốc đi nửa đường sau (đi 30 km sau) = x - 6
thời gian đi nửa đường sau = 30/(x -6)
Theo đề ta có
30/(x + 10) + 30/(x - 6) = 60/x
1/(x + 10) + 1/(x - 6) = 2/x
x(x-6) + x(x+10) = 2(x-6)
(x+10)x^2 - 6x + x^2 +10x = 2(x^2 + 4x - 60)
2x^2 + 4x = 2x^2 + 8x - 120
4x = 120
x = 30 (thỏa mãn)
Vậy thời gian dự định đi quãng đường AB là t = 60/x = 60/30 = 2 giờ

gọi vận tốc dự định đi quãng đường AB = x km/giờ (x>0)
thời gian dự định đi quãng đường AB = 60/x
--> vận tốc đi nửa đường đầu (đi 30km đầu) = x + 10
thời gian đi nửa đường đầu = 30/(x + 10)
--> vận tốc đi nửa đường sau (đi 30 km sau) = x - 6
thời gian đi nửa đường sau = 30/(x -6)
Theo đề ta có
30/(x + 10) + 30/(x - 6) = 60/x
1/(x + 10) + 1/(x - 6) = 2/x
x(x-6) + x(x+10) = 2(x-6)(x+10)
x^2 - 6x + x^2 +10x = 2(x^2 + 4x - 60)
2x^2 + 4x = 2x^2 + 8x - 120
4x = 120
x = 30 (thỏa)
Vậy thời gian dự định đi quãng đường AB là t = 60/x = 60/30 = 2 giờ

Giải:
Gọi vận tốc dự định đi quãng đường AB = x km/giờ (x>0)
thời gian dự định đi quãng đường AB = 60/x
--> vận tốc đi nửa đường đầu (đi 30km đầu) = x + 10
thời gian đi nửa đường đầu = 30/(x + 10)
--> vận tốc đi nửa đường sau (đi 30 km sau) = x - 6
thời gian đi nửa đường sau = 30/(x -6)
Theo đề ta có
30/(x + 10) + 30/(x - 6) = 60/x
1/(x + 10) + 1/(x - 6) = 2/x
x(x-6) + x(x+10) = 2(x-6)(x+10)
x^2 - 6x + x^2 +10x = 2(x^2 + 4x - 60)
2x^2 + 4x = 2x^2 + 8x - 120
4x = 120
x = 30 (thỏa)
Vậy thời gian dự định đi quãng đường AB là t = 60/x = 60/30 = 2 giờ

Gọi vận tốc ô tô dự định đi quãng đường AB là x (km/h).
Có phương trình: 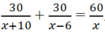
Giải ra được x = 30
Thời gian ô tô dự định đi là 2 giờ.

Sửa đề: AB dài 60km
Gọi x(km/h) là vận tốc dự định của ô tô(Điều kiện: x>0)
Thời gian dự định là: \(\dfrac{60}{x}\left(h\right)\)
Thời gian ô tô đi nửa quãng đường đầu là: \(\dfrac{30}{x+10}\left(h\right)\)
Thời gian ô tô đi nửa quãng đường sau là: \(\dfrac{30}{x-6}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{30}{x+10}+\dfrac{30}{x-6}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{30\left(x-6\right)+30\left(x+10\right)}{\left(x+10\right)\left(x-6\right)}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{60x+120}{\left(x+10\right)\left(x-6\right)}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{x\left(60x+120\right)}{x\left(x+10\right)\left(x-6\right)}=\dfrac{60\left(x+10\right)\left(x-6\right)}{x\left(x+10\right)\left(x-6\right)}\)
\(\Leftrightarrow60x^2+120x=60\left(x^2+4x-60\right)\)
\(\Leftrightarrow60x^2+120x-60x^2-240x+3600=0\)
\(\Leftrightarrow-120x=-3600\)
hay x=30(thỏa ĐK)
Vậy: Vận tốc dự định là 30km/h

Gọi vận tốc dự định đi là x (giờ)
Thời gian dự định là: \(\dfrac{60}{x}\)(km/h)
Thời gian nửa đầu là: \(\dfrac{30}{x}+10\)(km/h)
Thời gian nửa sau là: \(\dfrac{30}{x}-6\) (km/h)
Theo đề bài ta có PT:
\(\dfrac{30}{x}+10+\dfrac{30}{x}-6=\dfrac{60}{x}\)
Giải ra ta được x=30 (km/h)
Vậy thời gian đi là 60 :30 =2 giờ
Lời giải:
Giả sử vận tốc dự định là $a$ km/h. ĐK: $a>6$
Thời gian dự định: $\frac{60}{a}$.
Thời gian ô tô đi nửa quãng đường đầu: $\frac{30}{a-6}$ (h)
Thời gian ô tô đi nửa quãng đường sau: $\frac{30}{a+10}$ (h)
Vì ô tô vẫn đảm bảo thời gian dự định nên:
$\frac{30}{a-6}+\frac{30}{a+10}=\frac{60}{a}$
Với điều kiện $a>6$ ta dễ dàng giải ra $a=30$ (km/h)
Thời gian dự định là: $\frac{60}{a}=\frac{60}{30}=2$ (h)