Cho dãy số có quy luật như sau: 2,3,7,16,32,57,93,142...
Hãy tính tổng số hạng thứ 24 và số hạng 40 và tìm quy luật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quy luật: Dãy số cách đều, mỗi số cách nhau 2 đơn vị.
Ba số hạng tiếp theo của dãy là: - 12 ; - 10; - 8.
Tổng ba số hạng đó là: − 12 + − 10 + − 8 = − 30

Bài 2:
Số hạng thứ 100 là:
\(1+2\cdot\left(100-1\right)=1+2\cdot99=199\)

\(3=2^2-1\)
\(8=3^2-1\)
\(15=4^2-1\)
\(24=5^2-1\)
...
Do đó quy luật của dãy là: \(a_n=\left(n+1\right)^2-1\) với n là số hạng thứ n của dãy
Do đó số hạng thứ 40 là: \(a_{40}=\left(40+1\right)^2-1=41^2-1=1680\)
Số hạng thứ 53 là: \(\left(53+1\right)^2-1=2915\)

a: Quy luật là Un=1/n(n+1)
1/42; 1/56; 1/72
b: Số thứ 50 là 1/50*51=1/2550
Tổng là:
1/2+1/6+...+1/2550
=1-1/2+1/2-1/3+...+1/50-1/51
=1-1/51
=50/51


Nhận xét : 0 = 1x1x1-1
6 = 2x2x2-2
24 = 3x3x3-3
60 = 4x4x4-4
QL: Số thứ m = mxmxm-m
Vậy số thứ 100 là : 100x100x100-100 = 999900

quy luật là
3=3x1
8=4x2
15=5x3
24=6x4
số thứ 50 là
7x5=35
8x6=48
9x7=63
vậy số thứ 50 là 63
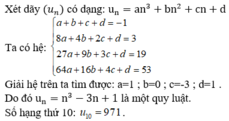
Sửa lại:
Số hạng thứ 24: 4902
Số hạng thứ 40: 22142
-Quy luật:
Một số hạng ở vị trí n bằng tổng của n2 và số hạng ở vị trí n-1.
\(\left(a_n=n^2+a_{n-1}\right)\) (với n∈N*)
Hoặc \(a_n=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+2\)
Số hạng thứ 24: 4907.
Số hạng thứ 40: 23736.
-Quy luật: Một số hạng ở vị trí n bằng tổng của n2 và số hạng ở vị trí n-1.
\(\left(a_n=n^2+a_{n-1}\right)\)