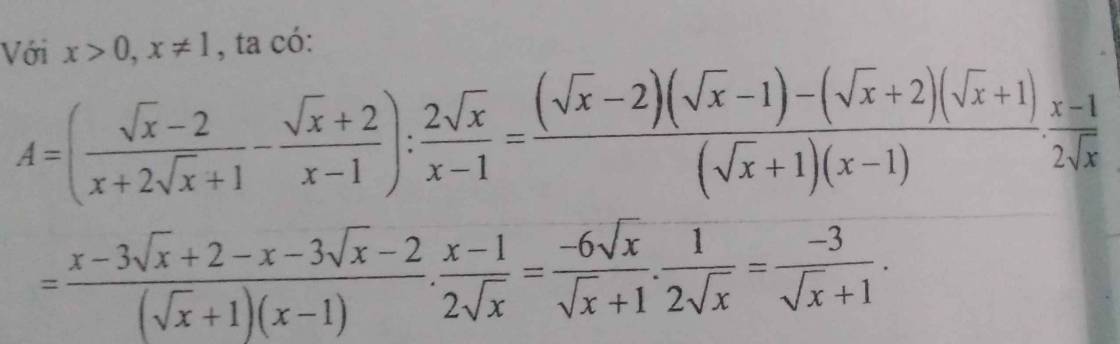Cho em hỏi bài 5.90 làm sao vậy ạ ??
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LN
Lê Ng Hải Anh
12 tháng 4 2021
Đúng(1)
Những câu hỏi liên quan
PA
2
NH
1
4 tháng 5 2021
Giải:
a) Vì Om là tia p/g của xÔy
⇒xÔm=mÔy=xÔy/2=40o/2=20o
Vì On là tia p/g của xÔz
⇒xÔn=nÔz=xÔz/2=120o/2=60o
⇒xÔy+yÔn=xÔn
40o +yÔn=60o
yÔn=60o-40o
yÔn=20o
⇒mÔy+yÔn=mÔn
20o +20o =mÔn
⇒mÔn=40o
b) Vì +) mÔy+yÔn=mÔn
+) mÔy=yÔn=20o
⇒Oy là tia p/g của mÔn
c) Vì tia Ot là tia đối của tia Oy
⇒yÔt=180o
Vì +) Oy;Oz cùng ∈ 1 nửa mặt phẳng có bờ chứa tia Ox
+) xÔy<xÔz (40o<120o)
⇒Oy nằm giữa Ox và Oz
⇒xÔy+yÔz=xÔz
40o+yÔz=120o
yÔz=120o-40o
yÔz=80o
⇒yÔz+zÔt=180o (2 góc kề bù)
80o+zÔt=180o
zÔt=180o-80o
zÔt=100o
Chúc bạn học tốt!
T
1
Y
31 tháng 5 2023
Mình giải thích từ dấu tương đương 2 nha.
\(\dfrac{2x\left(x-2\right)+2x}{2x\left(x-1\right)\left(x-2\right)}=\dfrac{3\left(x-1\right)\left(x-2\right)}{2x\left(x-1\right)\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{2x^2-4x+2x}{2x\left(x-1\right)\left(x-2\right)}-\dfrac{3\left(x-1\right)\left(x-2\right)}{2x\left(x-1\right)\left(x-2\right)}=0\)
\(\Leftrightarrow\dfrac{2x^2-2x-3\left(x^2-2x-x+2\right)}{2x\left(x-1\right)\left(x-2\right)}=0\)
Tới đây phải khử mẫu pt bằng cách lấy mẫu \(2x\left(x-1\right)\left(x-2\right)\) nhân với 0 bên vế phải thì pt mới đơn giản để giải tiếp được.
\(\Leftrightarrow2x^2-2x-3x^2+6x+3x-6=0\)
\(\Leftrightarrow2x^2-2x=3x^2-9x+6\)
Tới đây là ra được dấu tương đương 3 rồi đó.
OP
15
24 tháng 1 2022
thì cứ ghi thêm vèo thôi chứ seo :") đòi viết như thế nào nữa
21 tháng 11 2021
BẠN NHẤP VÀO TÊN CỦA MÌNH BÊN CẠNH PHẦN HỖ TRỢ TRƯỜNG HỌC Í, RỒI NHẤN THOÁT
@Bùi Thị Bảo Châu
From Ŧŗịɳħ Đüć Ťĭếɳ ( teamღVTP )
Y
6 tháng 6 2023
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}^2+2\sqrt{x}+1^2}-\dfrac{\sqrt{x}+2}{\sqrt{x}^2-1^2}\right).\dfrac{x-1}{2\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{x-1}{2\sqrt{x}}\)
Tới đây là có được mẫu chung ở dấu = thứ 2 rồi.
LD
6 tháng 6 2023
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\) ( với x>0;\(x\ne1\) )
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right].\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}.\dfrac{x-1}{2\sqrt{x}}\)
\(=.....\) ( theo như trên )
