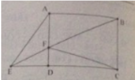
Cho hình chữ nhật ABCD có chiều dài 7cm, rộng 5cm. Trên AD chọn điểm F sao cho AF=3cm. Nối BF cắt đoạn CD kéo dài tại E. Tính diện tích AEF và EFC. (Hãy nhớ đây có 2 câu hỏi AEF VÀ EFC, KHÔNG PHẢI CHỈ CÓ AEF.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AB và CD song song nhau,nếu lấy F trên AB thì không thể cho BF cắt CD được :

Giải Ta có:
S(ABE) = S(ABC) = ½ AB
BC = 17,5 (cm²) S(ABF) = ½ AB AF = 10,5 (cm²)
Suy ra diện tích tam giác AEF là
S(AEF) = S(ABE) – S(ABF) = 17,5 – 10,5 = 7 (cm²)
Đáp số: 7 cm².
Tam giác EAB cạnh đáy BA chiều cao nằm ngoài tam giác và cũng chính bằng chiều rộng BC của hình chữ nhật = 5cm.
Diện tích hình tam giác EBA là: 7 x 5 : 2 = 17,5 cm2
Diẹn tích hình tam giác FAB là: 3 x 7:2 = 10,5cm2
Diễn tích hình tam giác AEF: 17,5 - 10,5 = 7cm2
Đáp số: 7cm2
~ học tốt~

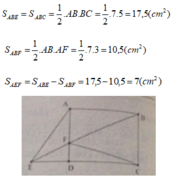
Ta có: S(ABE) = S(ABC) = ½ AB BC = 17,5 (cm²)
S(ABF) = ½ AB AF = 10,5 (cm²)
Suy ra diện tích tam giác AEF là
S(AEF) = S(ABE) – S(ABF) = 17,5 – 10,5 = 7 (cm²)
Đáp số: 7 cm².
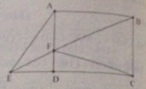
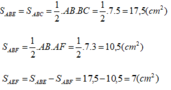
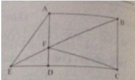
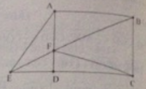
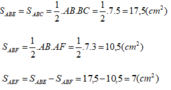
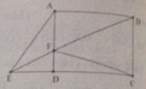
Vì đề bài không rõ ràng AD là chiều dài hay chiều rộng nên trong bài này tôi coi AD là chiều rông.
\(S_{ABCD}=ADxAB=5x7=35cm^2\)
Ta có \(S_{ABC}=\dfrac{1}{2}xS_{ABCD}\)
Hai tg ABC và tg FBC có chung BC, đường cao từ A->BC = đường cao từ F->BC nên
\(S_{FBC}=S_{ABC}=\dfrac{1}{2}xS_{ABCD}\)
Hai tg ABF và tg FBC có đường cao từ B->AD = đường cao từ F->BC nên
\(\dfrac{S_{ABF}}{S_{FBC}}=\dfrac{AF}{BC}=\dfrac{3}{5}\Rightarrow S_{ABF}=\dfrac{3}{5}xS_{FBC}=\dfrac{3}{5}x\dfrac{1}{2}xS_{ABCD}=\dfrac{3}{10}xS_{ABCD}\)
Hai tg này có chung BF nên
\(\dfrac{S_{ABF}}{S_{FBC}}=\) đường cao từ A->BE / đường cao từ C->BE \(=\dfrac{3}{5}\)
=> đường cao từ A->BE = \(\dfrac{3}{5}\) đường cao từ C->BE
Hai tg AEF và tg DEF có chung đường cao từ E->AB nên
\(\dfrac{S_{AEF}}{S_{DEF}}=\dfrac{AF}{DF}=\dfrac{3}{2}\)
Hai tg này có chung EF nên
\(\dfrac{S_{AEF}}{S_{DEF}}=\) đường cao từ A->BE / đường cao từ D->BE\(=\dfrac{3}{2}\)
=> đường cao từ D->BE = \(\dfrac{2}{3}\) đường cao từ A-> BE = \(\dfrac{2}{3}x\dfrac{3}{5}\) đường cao từ C->BE \(=\dfrac{2}{5}\) đường cao từ C->BE
Hai tg DEF và tg CEF có chung EF nên
\(\dfrac{S_{DEF}}{S_{FCE}}=\)đường cao từ D->BE / đường cao từ C->BE \(=\dfrac{2}{5}\)
Chia diện tích tg DEF thành 2 phần thì diện tích tg CEF là 5 phần
=> Số phần chỉ diện tích tg CDF là
5-2=3 phần
\(\Rightarrow\dfrac{S_{DEF}}{S_{CDF}}=\dfrac{2}{3}\)
Hai tg này có chung DF nên
\(\dfrac{S_{DEF}}{S_{CDF}}=\) đường cao từ E->AD / đường cao từ C->AD \(=\dfrac{2}{3}\)
Mà đường cao từ C->AD = đường cao từ B->AD
=> đường cao từ E->AD / đường cao từ B->AD = \(\dfrac{2}{3}\)
Hai tg AEF và tg ABF có chung AF nên
\(\dfrac{S_{AEF}}{S_{ABF}}=\)đường cao từ E->AD / đường cao từ B->AD \(=\dfrac{2}{3}\)
\(\Rightarrow S_{AEF}=\dfrac{2}{3}xS_{ABF}=\dfrac{2}{3}x\dfrac{3}{10}xS_{ABCD}=\dfrac{1}{5}xS_{ABCD}=\dfrac{1}{5}x35=7cm^2\)
Hai tg AEF và tg EFC có chung EF nên
\(\dfrac{S_{AEF}}{S_{EFC}}=\)đường cao từ A->BE / đường cao từ C->BE \(=\dfrac{3}{5}\)
\(\Rightarrow S_{EFC}=\dfrac{5}{3}xS_{AEF}=\dfrac{5}{3}x7=\dfrac{35}{3}cm^2\)