Cho tam giác ABC vuông tại A, AB = 9 cm, BC = 15 cm. Trên tia đối của tia AB lấy điểm E sao cho A là trung điểm của BE.a) Chứng minh rằng ΔABC=ΔAEC.ΔABC=ΔAEC.b) Vẽ đường trung tuyến BH của ΔBECΔBEC cắt cạnh AC tại M. Chứng minh M là trọng tâm của ΔBECΔBEC và tính độ dài đoạn CM.c) Từ A vẽ đường thẳng song song với EC, đường thẳng này cắt cạnh BC tại K. Chứng minh rằng ba điểm E, M, K thẳng...
Đọc tiếp
Cho tam giác ABC vuông tại A, AB = 9 cm, BC = 15 cm. Trên tia đối của tia AB lấy điểm E sao cho A là trung điểm của BE.
a) Chứng minh rằng ΔABC=ΔAEC.ΔABC=ΔAEC.
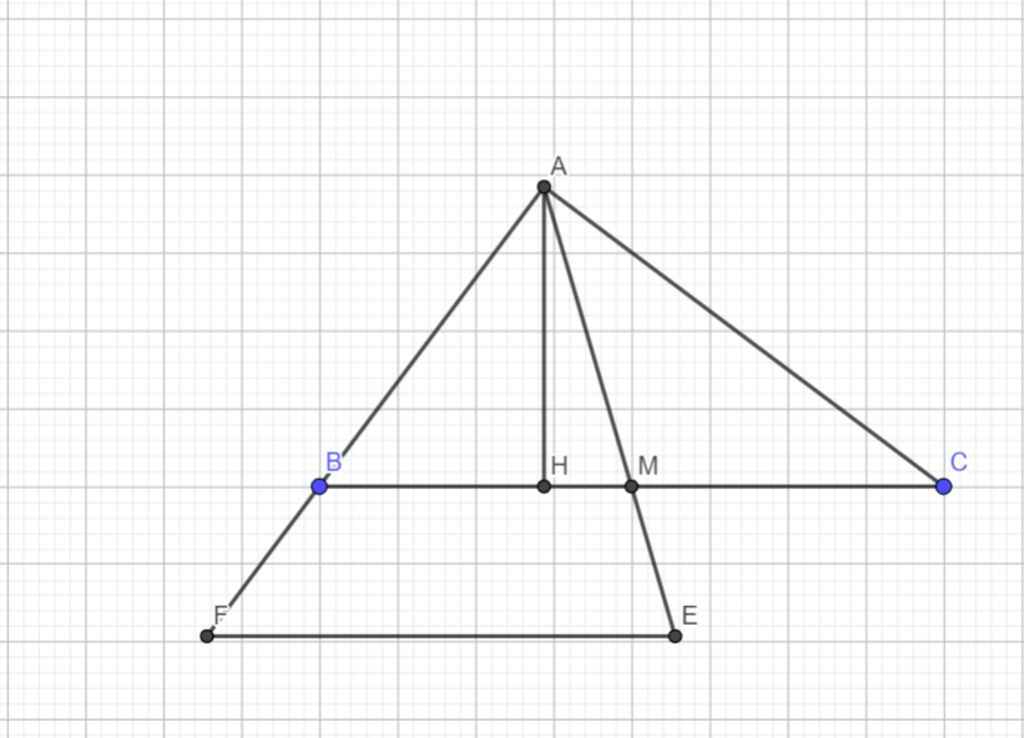
b) Vẽ đường trung tuyến BH của ΔBECΔBEC cắt cạnh AC tại M. Chứng minh M là trọng tâm của ΔBECΔBEC và tính độ dài đoạn CM.
c) Từ A vẽ đường thẳng song song với EC, đường thẳng này cắt cạnh BC tại K. Chứng minh rằng ba điểm E, M, K thẳng hàng.
Tham khảo
a) Áp dụng định lí Pi - ta - go vào t/giác ABC vuông tại A, ta có:
BC^2 = AB^2 + AC^2
=> AC^2 = BC^2 - AC^2 = 15^2 - 9^2 = 225 - 81 = 144
=> AC = 12 (cm)
Ta có: AB < AC < BC (9 cm < 12 cm < 15 cm)
=> góc C < góc B < góc A (quan hệ giữa cạnh và góc đối diện)
b) Xét t/giác ABC và t/giác AEC
có: AB = AE (gt)
góc BAC = góc CAE = 90 độ (gt)
AC : chung
=> t/giác ABC = t/giác AEC (c.g.c)
Tham khảo:
a) Xét ΔABCΔABC vuông tại A và ΔAECΔAEC vuông tại A có:
AB = AE (theo giả thiết)
AC chung
⇒ΔABC=ΔAEC⇒ΔABC=ΔAEC (2 cạnh góc vuông)
b) Do A là trung điểm của BE nên CA là đường trung tuyến ứng của
Xét ΔBECΔBEC có CA và BH là hai đường trung tuyến cắt nhau tại M.
Do đó M là trọng tâm của ΔBECΔBEC
Do đó CM = 2323CA.
Áp dụng định lý Pytago vào vuông tại A:
AB2 + AC2 = BC2
92 + AC2 = 152
AC2 = 225 - 81
AC2 = 144
AC = 12 cm
Khi đó CM = CA = .12 = 8 cm.
Vậy CM = 8 cm.
c) Trên tia đối của tia KA lấy điểm N sao cho KN = KA.
Do ΔABC=ΔAECΔABC=ΔAEC (2 cạnh góc vuông) nên BC = EC (2 cạnh tương ứng) và ˆACB=ˆACEACB^=ACE^ (2 góc tương ứng).
⇒ˆKCA=ˆACE⇒KCA^=ACE^.
Do AK // EC nên ˆKAC=ˆACEKAC^=ACE^ (2 góc so le trong)
Do đó ˆKCA=ˆKACKCA^=KAC^.
ΔKACΔKAC có ˆKCA=ˆKACKCA^=KAC^ nên ΔKACΔKAC cân tại K.
Do đó KA = KC.
Mà KA = KN = 1212 AN nên KA = KN = KC = 1212 AN.
có KA = KN = KC = 1212 AN nên vuông tại C.
Xét ΔACNΔACN vuông tại C và ΔCAEΔCAE vuông tại A:
ˆNAC=ˆECANAC^=ECA^ (chứng minh trên).
AC chung.
⇒ΔACN=ΔCAE⇒ΔACN=ΔCAE (góc nhọn - cạnh góc vuông).
⇒⇒ AN = CE (2 cạnh tương ứng).
Mà EC = BC nên AN = BC.
Mà AN = 2AK nên BC = 2AK.
Lại có AK = KC nên BC = 2KC.
Do đó K là trung điểm của BC.
ΔBECΔBEC có M là trọng tâm, lại có K là trung điểm của BC nên E, M, K thẳng hàng.
Vậy E, M, K thẳng hàng.