Cho tam giác ABC cân tại A có hai đường trung tuyến BD và EC cắt nhau tại G.
a) Chứng minh BD=CE
b) chứng minh tam giác ABD là tam giác cân
c) Chứng minh GD+GE>1/2 BC
giúp mình với ạ, cảm ơn rất nhiều=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2023
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
=>ΔADB=ΔAEC
b: Xet ΔEBC và ΔDCB có
EB=DC
góc EBC=góc DCB
BC chung
=>ΔEBC=ΔDCB
=>góc GBC=góc GCB
=>ΔGBC cân tại G
S
4 tháng 3 2023
xét ΔECB và ΔDBC, ta có :
EC = BD (gt)
\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)
BC là cạnh chung
=> ΔECB = ΔDBC (c.g.c)
=> \(\widehat{GBC}=\widehat{GCB}\) (2 góc tương ứng)
vì ΔGBC có \(\widehat{GBC}=\widehat{GCB}\) nên ⇒ ΔGBC là một tam giác cân (cân tại G)
12 tháng 5 2023
Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
=>ΔABD=ΔACE
Sửa đề: ΔGBC cân tại G
Xét ΔEBC và ΔDCB có
EB=DC
góc EBC=góc DCB
BC chung
=>ΔEBC=ΔDCB
=>góc GBC=góc GCB
=>ΔGBC cân tại G
18 tháng 3 2021
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)
Xét ΔBDC vuông tại D và ΔCEB vuông tại E có
BC chung
BD=CE(ΔABD=ΔACE)
Do đó: ΔBDC=ΔCEB(cạnh huyền-cạnh góc vuông)
17 tháng 3 2023
a: G là trọng tâm
=>BG=2/3BD; CG=2/3CE
=>BG=CG
=>DG=GE
b: Xet ΔEBC và ΔDCB có
BC chung
góc ECB=góc DBC
EC=BD
=>ΔEBC=ΔDCB
=>góc ABC=góc ACB
=>ΔACB cân tại A
26 tháng 3 2021
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE(Cạnh huyền-góc nhọn)
7 tháng 4 2021
A) XÉT ΔABD VUÔNG TẠI D, ΔACE VUÔNG TẠI E
CÓ; AB=AC (ΔABC CÂN TẠI A)
\(\widehat{BAC}\) : GÓC CHUNG
⇒ΔABD= ΔACE (C.HUYỀN-G.NHỌN)
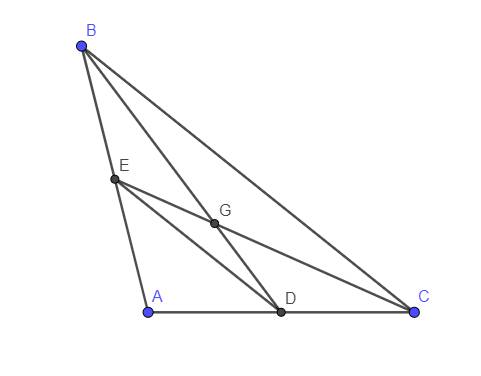
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{BAD}\) chung
AD=AE
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
nên AD=AE
hay ΔADE cân tại A
refer
a: Xét ΔABD và ΔACE có
AB=AC
ˆBADBAD^ chung
AD=AE
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
nên AD=AE
hay ΔADE cân tại A