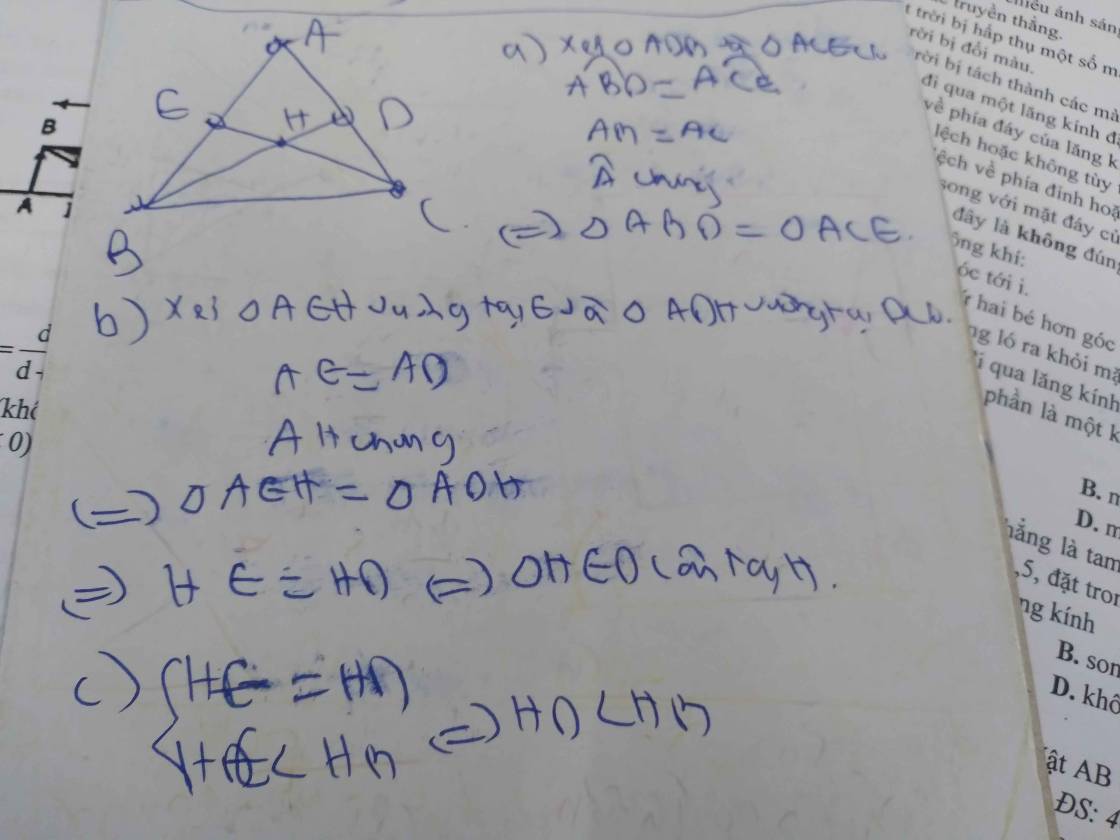
Cho ΔABC cân tại A ,hai đường cao AI và BD cắt nhau tại H.
a) Chứng minh rằng :ΔAIC ∼ ΔBDC.
b) Gọi E là giao điểm của CH và AB.Chứng minh BE.BA + CH.CE = BC2.
c) Gọi T là giao điểm của DE và AH.Chứng minh \(\dfrac{1}{AT}\) + \(\dfrac{1}{AI}\) = \(\dfrac{2}{AH}\)