Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Tính góc giữa mp ( SAB) và mp (SBC). b) Tính khoảng cách từ A đến mp ( SBD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ

a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)

Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)

Bạn kiểm tra lại đề,
1. ABCD là hình thang vuông tại A và B hay A và D? Theo dữ liệu này thì ko thể vuông tại B được (cạnh huyền DC nhỏ hơn cạnh góc vuông AB là cực kì vô lý)
2. SC và AC cắt nhau tại C nên giữa chúng không có khoảng cách. (khoảng cách bằng 0)
Nguyễn Việt Lâm
e xin loi a
ABCD là hình thang vuông tại A và D
còn đoạn sau khoảng cách giữa 2 đt SC và AC thì e kh biet no sai o đau
anh giup em vs ah

Đáp án A
Từ giả thiết ta có:
![]()
=> AB = SA = 2a =>
V
S
.
BDM
=
(
1
/
4
)
V
S
.
ABCD
=
a
3
/
3
Mặt khác ta có:
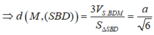
SB = 2a
2
; SD = a
5
; BD = a
5
=> SΔSBD =
a
2
6

1: AC=căn a^2+a^2=a*căn 2
=>SC=căn SA^2+AC^2=a*căn 8
SB=căn AB^2+SA^2=a*căn 7
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
=>SB vuông góc BC

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(SO\in\left(SAC\right)\Rightarrow BD\perp SO\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AO\) là hình chiếu vuông góc của SO lên (ABCD)
\(\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{6}\Rightarrow\widehat{SOA}\approx67^047'\)

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
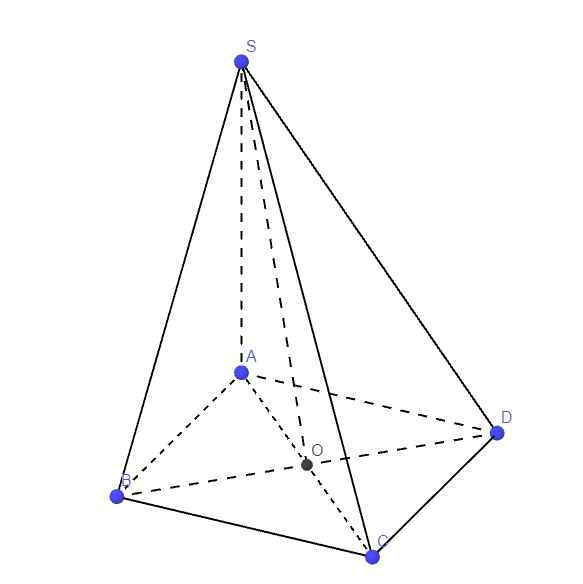
Tuy nhiên đề cho giá trị cạnh AC với BC bị sai. Cạnh huyền AC (\(a\sqrt{3}\)) sao lại có giá trị nhỏ hơn cạnh góc vuông BC (2a) nhỉ?