Cho △ABC có \(\widehat{A}\)=45 độ, \(\widehat{B}\)=75 độ thì:
a. BC<AB<AC
b. BC<AC<AB
c. AB<AC<BC
d. AC<BC<AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BA
9 tháng 11 2019
Ta có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^O\)
\(\Rightarrow\widehat{C}=180^O-\widehat{A}-\widehat{B}\)
\(\Rightarrow\widehat{C}=180-75-65=40\)
Vì AD là tia phân giác của góc A
\(\Rightarrow\hept{\begin{cases}A_1=37,5\\A_2=37,5\end{cases}}\)
Ta có
\(A_1+C+D_1=180\)
\(\Rightarrow D_1=180-C-A_1\)
\(\Rightarrow D_1=180-40-37,5=102,5^O\)
Tương tự \(\Delta ABD\)ta có
\(D_1=77,5^o\)
Vậy......
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
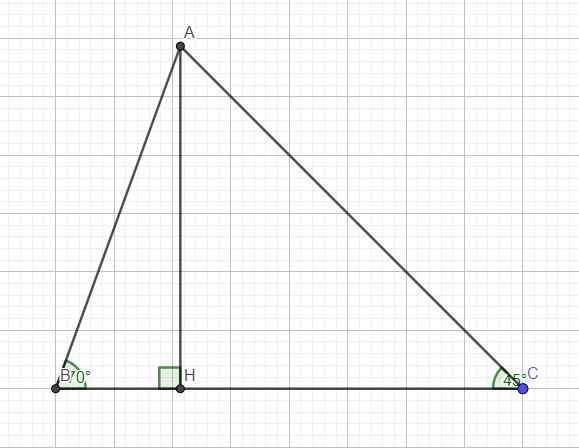
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
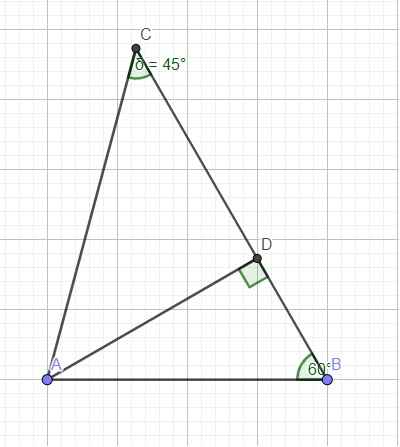
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
12 tháng 4 2017
Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{A}=75^o\)
* \(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\Rightarrow AB=\dfrac{BCsinC}{sinA}=a\left(1+\sqrt{3}\right)\)
* \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\Rightarrow AC=\dfrac{BCsinB}{sinA}=a\left(\dfrac{-6+3\sqrt{2}}{2}\right)\)
chọn A
A