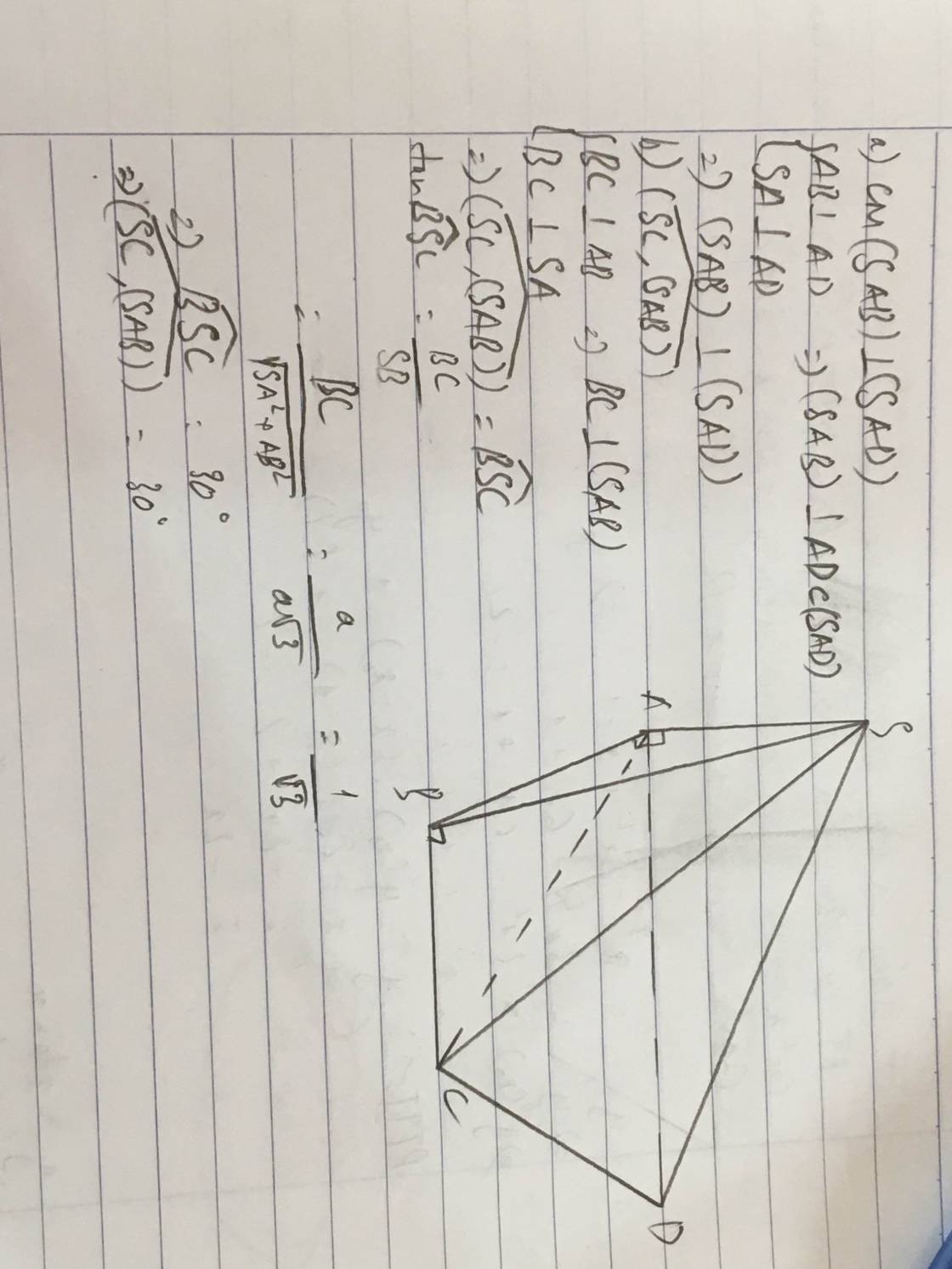
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại A và B, Kẻ $SA$ vuông góc với $mp\left(ABCD\right)$. Biết rằng $AB=BC=a$, $AD=2a$ góc giữa $SB$ và \(mp\left(A...

PK

Phạm Kim Oanh

10 tháng 5 2022

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại A và B, Kẻ $SA$ vuông góc với $mp\left(ABCD\right)$. Biết rằng $AB=BC=a$, $AD=2a$ góc giữa $SB$ và $mp\left(ABCD\right)$ bằng $45^0$a) Chứng minh rằng BC vuông góc với SB, và $mp\left(SCD\right)\perp mp\left(SAC\right)$b) Gọi $mp\left(\alpha\right)$ là mặt phẳng đi qua A và vuông góc với SC. Xác định thiết diện của hình chóp $S.ABCD$ ...

Đọc tiếp

#Toán lớp 11

0

NH

Nguyễn Hoàng Anh

3 tháng 3 2022

Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB. SA vuông góc với (ABCD) a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)

#Toán lớp 11

4

NV

Nguyễn Việt Lâm

Giáo viên

3 tháng 3 2022

a.

$\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.$ $\Rightarrow CD\perp\left(SAD\right)$

Mà $CD=\left(SCD\right)\cap\left(ABCD\right)$

$\Rightarrow\widehat{SDA}$ là góc giữa (SCD) và (ABCD)

$tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0$

b.

Gọi E là giao điểm AC và DI

I là trung điểm AB $\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC$

$\Rightarrow AICD$ là hình bình hành

Mà $\widehat{A}=90^0\Rightarrow AICD$ là hình chữ nhật

$AI=AD=a$ (hai cạnh kề bằng nhau) $\Rightarrow AICD$ là hình vuông

$\Rightarrow AC\perp DI$ tại E

Lại có $SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)$

Mà $DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}$ là góc giữa (SDI) và (ABCD)

$AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}$

$\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'$

Đúng(2)

G

Gallavich

3 tháng 3 2022

https://hoc24.vn/cau-hoi/.5005119341955 tương trợ em với thầy :((

Đúng(0)

PK

Phạm Kim Oanh

23 tháng 5 2022

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$. Biết rằng $SA\perp mp\left(ABCD\right)$ , gọi M là hình chiếu vuông góc của $A$ lên cạnh $SD$ . Giả sử rằng $AB=2.AD=2.DC=2.a$ , độ dài cạnh $SA=2a$ Tính khoảng cách từ điểm $M$ đến $mp\left(SBC\right)$P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạEm cám ơn nhiều...

Đọc tiếp

#Toán lớp 11

0

JE

Julian Edward

21 tháng 4 2021

Cho hình chóp S.ABCD có SA vuông góc với mp đáy (ABCD) và ABCD là hình thang vuông tại A, đáy lớn AB, AB=2a, AD=CD=a. Gọi H là hình chiếu vuông góc của A lên SC và E là trung điểm của ABa, CMR: (SCD) ⊥(SAD) và AH ⊥(SBC)b, Biết góc giữa 2 mp (SCD) và (ABCD) bằng 300. Tính góc giữa 2 mp (SAD) và...

Đọc tiếp

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

21 tháng 4 2021

$\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.$ $\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)$

$AC=\sqrt{AD^2+CD^2}=a\sqrt{2}$

$BC=\sqrt{BE^2+CE^2}=a\sqrt{2}$

$\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC$

$\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)$

b.

$CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}$ là góc giữa (SCD) và (ABCD)

$\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}$

Ta có: $\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.$ $\Rightarrow AD\perp\left(SAB\right)$

Qua S kẻ đường thẳng d song song AD

Do $AD||CE$ $\Rightarrow$ d là giao tuyến (SAD) và (SCE)

Mà $d\perp\left(SAB\right)\Rightarrow\widehat{ASE}$ là góc giữa (SAD) và (SCE)

$AE=\dfrac{AB}{2}=a$

$tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0$

Đúng(2)

JE

Julian Edward

21 tháng 4 2021

$tan\widehat{ASE}=\sqrt{3}$ chứ aj?

Đúng(0)

NH

Nguyễn Hoàng Anh

3 tháng 3 2022

Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

3 tháng 3 2022

Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)

Đúng(0)

NH

Nguyễn Hoàng Anh

3 tháng 3 2022

Vậy nếu SA vuông góc với đáy sẽ giải sao ạ ?

Đúng(0)

YP

Yeon Park

13 tháng 3 2022

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).

#Toán lớp 11

1

AM

Ami Mizuno

13 tháng 3 2022

undefined

Đúng(3)

HA

Hoàng Anh

14 tháng 3 2022

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, đáy lớn BC=2a, AB=AD=a, SB vuông góc (ABCD), SB= a√3 a. CM ∆SAD vuông b. CM DC vuông góc (SBD) c. Gọi O là giao điểm của AC và BD, (alpha) là mp qua O và vuông góc với AB. Tìm và tính thiết diện của hình chóp cắt bởi (alpha)Giúp mình với mn ơi...

Đọc tiếp

#Toán lớp 11

0

PL

Phương Lee

16 tháng 4 2021

1.Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB= $\dfrac{a\sqrt{3}}{3}$, AD=a$\sqrt{3}$, SA=a và vuông góc với mp đáy. Khi đó góc giữa SB và mp (SAD) bằng bao nhiêu?2.Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. SA vuông góc với mp đáy. Số mặt của tứ diện là tam giác vuông là bao nhiêu?3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, CA=a, CB=b, SA=h vuông góc với mặt đáy. Gọi I là trung điểm của AB.a, CMR: BC vuông...

Đọc tiếp

#Toán lớp 11

2

NV

Nguyễn Việt Lâm

Giáo viên

18 tháng 4 2021

1.

$\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AD\perp AB\end{matrix}\right.$ $\Rightarrow AB\perp\left(SAD\right)$

$\Rightarrow\widehat{SBA}$ là góc giữa SB và (SAD)

$tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{3}\Rightarrow\widehat{SBA}=60^0$

2.

$SA\perp\left(ABC\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AB\\SA\perp AC\end{matrix}\right.$ $\Rightarrow$ các tam giác SAB và SAC vuông

$\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.$ $\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB$

$\Rightarrow$ Tam giác SBC vuông

Vậy tứ diện có 4 mặt đều là tam giác vuông (ABC hiển nhiên vuông theo giả thiết)

Đúng(2)

NV

Nguyễn Việt Lâm

Giáo viên

17 tháng 4 2021

3.

a.

$\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AC\end{matrix}\right.$ $\Rightarrow BC\perp\left(SAC\right)$

b.

Gọi M là trung điểm BC $\Rightarrow IM||AC$

$\Rightarrow AC||\left(SIM\right)\Rightarrow d\left(AC;SI\right)=d\left(AC;\left(SIM\right)\right)=d\left(A;\left(SIM\right)\right)$

Qua A kẻ đường thẳng song song BC cắt IM kéo dài tại K

$\Rightarrow IM\perp AK\Rightarrow IM\perp\left(SAK\right)$

Trong mp (SAK), kẻ AH vuông góc SK

$\Rightarrow AH\perp\left(SIM\right)\Rightarrow AH=d\left(A;\left(SIM\right)\right)$

$AK=CM=\dfrac{b}{2}$

$\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AK^2}\Rightarrow AH=\dfrac{SA.AK}{\sqrt{SA^2+AK^2}}=\dfrac{\dfrac{h.b}{2}}{\sqrt{h^2+\dfrac{b^2}{4}}}=\dfrac{bh}{\sqrt{b^2+4h^2}}$

Đúng(2)

NL

Nguyễn Lê Phước Thịnh

8 tháng 5 2023

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết AB=2a, AD=DC=a. Cạnh bên SA vuông góc với đáy và $SA=a\sqrt{2}$. CHọn khẳng định sai?A: $\widehat{\left(SBC\right);\left(ABCD\right)}=45^0$B: $\widehat{\left(SDC\right);\left(BCD\right)}=60^0$C: Giao tuyến của (SAB) với (SCD) song song...

Đọc tiếp

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

8 tháng 5 2023

B là khẳng định sai

$\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.$ $\Rightarrow CD\perp\left(SAD\right)$

$CD=\left(SCD\right)\cap\left(BCD\right)$

$\Rightarrow\widehat{SDA}$ là góc giữa (SDC) và (BCD)

$tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'$

Đúng(2)

TC

Thầy Cao Đô

Giáo viên VIP

27 tháng 4 2022 - olm

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $B$, $BA=BC=a$, $AD=2a$. Cạnh bên $SA$ vuông góc với mặt đáy và $SA=a\sqrt{2}$. a) (1 điểm) Chứng minh $\left( SAB \right) \perp \left( SAD \right)$. b) (1 điểm) Tính góc giữa đường thẳng $SC$ và mặt phẳng $\left( SAB \right)$. c) (1 điểm) Gọi $H$ là hình chiếu vuông góc của $A$ lên $SB$. Tính khoảng cách từ $H$ đến mặt phẳng $\left( SCD...

Đọc tiếp

#Toán lớp 11

12