cho nửa đường tròn (0) , đường kính AB.C là 1 điểm nằm giữa O và A.Đường thẳng vuông góc với AB tại C cắt nửa đường tròn (0) tại I . M là 1 điểm bất kì kì thuộc cung DI(M≠B và I) , tia Am cắt CI tại K , tia BM cát CI tại D . Chứng Minh:a) Tứ Giác BMKC nội tiếp đường trònb)Góc BAD=góc BMC và...
Đọc tiếp
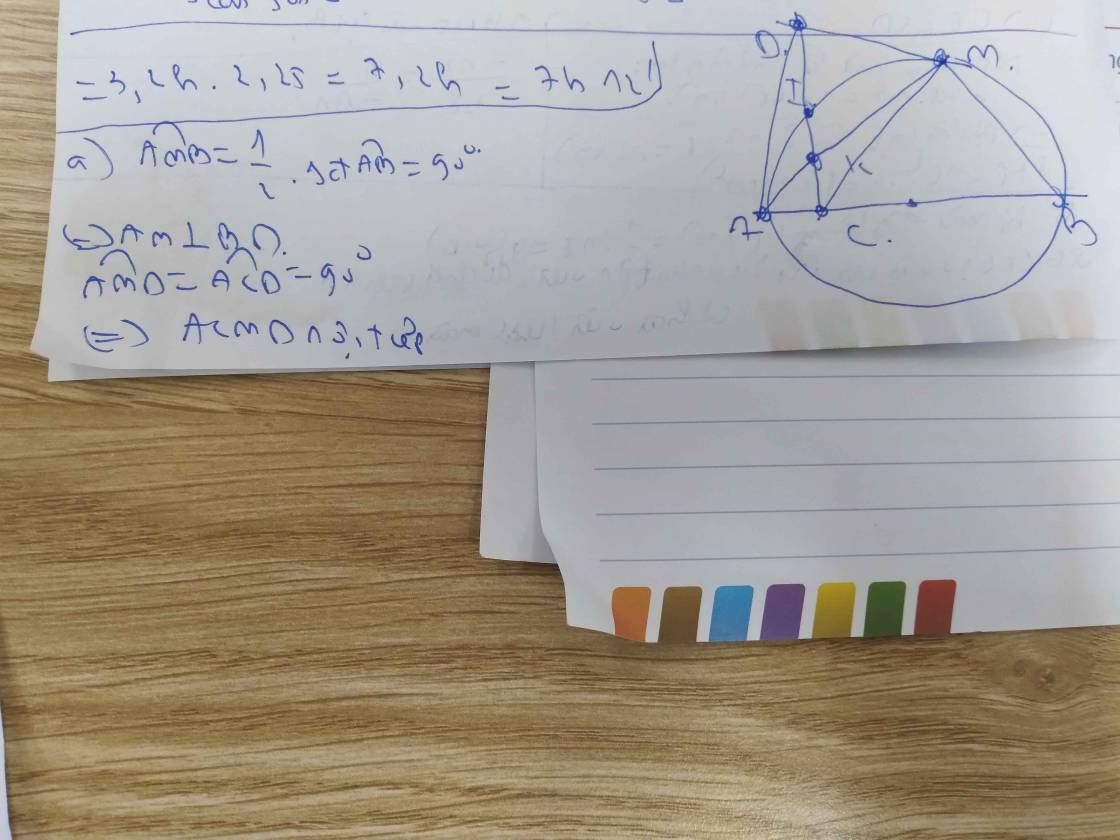
cho nửa đường tròn (0) , đường kính AB.C là 1 điểm nằm giữa O và A.Đường thẳng vuông góc với AB tại C cắt nửa đường tròn (0) tại I . M là 1 điểm bất kì
kì thuộc cung DI(M≠B và I) , tia Am cắt CI tại K , tia BM cát CI tại D . Chứng Minh:
a) Tứ Giác BMKC nội tiếp đường tròn
b)Góc BAD=góc BMC và BD.MC=BC.AD
a: Xét tứ giác BMKC có \(\widehat{BMK}+\widehat{KCB}=180^0\)
nên BMKC là tứ giác nội tiếp
b: Xét ΔBMA vuông tại M và ΔBCD vuông tại C có
góc B chung
Do đó: ΔBMA\(\sim\)ΔBCD
Suy ra: BM/BC=BA/BD
hay BM/BA=BC/BD
=>ΔBMC\(\sim\)ΔBAD
nên \(\widehat{BMC}=\widehat{BAD}\)