Cho các số thực dương a,b,c thoả mãn a + b + c = 3. tìm giá trị lớn nhất của P = √a+b + √b+c + √c + a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(P^2=\left(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\right)^2\le\left(a+b+b+c+c+a\right)\left(1^2+1^2+1^2\right)\)
\(=6\left(a+b+c\right)=18\)
Suy ra \(P\le3\sqrt{2}\)
Dấu \(=\) xảy ra khi \(a=b=c=1\).

Áp dụng BĐT Bunhiacopxky :
\(\left(9a^3+3b^2+c\right)\left(\frac{1}{9a}+\frac{1}{3}+c\right)\ge\left(a+b+c\right)^2=1\)
\(\Rightarrow9a^3+3b^2+c\ge\frac{1}{\frac{1}{9a}+\frac{1}{3}+c}\)
\(\Rightarrow\frac{a}{9a^3+3b^2+c}\le a\left(\frac{1}{9a}+\frac{1}{3}+c\right)\)
Thực hiện tương tự với các phân thức khác và cộng theo vế :
\(P\le\frac{1}{9}+\frac{1}{9}+\frac{1}{9}+\frac{a+b+c}{3}+\left(ab+bc+ac\right)\)
\(P\le\frac{2}{3}+ab+bc+ac\)
Theo hệ quả quen thuộc của BĐT AM - GM :
\(ab+bc+ac\le\frac{\left(a+b+c\right)^2}{3}=\frac{1}{3}\)
\(\Rightarrow P\le\frac{2}{3}+\frac{1}{3}=1\Rightarrow P_{max}=1\)
Vậy GTLN của P là 1 khi \(a=b=c=\frac{1}{3}\)


Ồ sorry bạn nhiều, chỗ đấy bị lỗi kĩ thuật rồi, mình sửa lại nhé :
\(M\ge\frac{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}{2\left(ab+bc+ca\right)}=\frac{\left(ab+bc+ca\right)^2}{2\left(ab+bc+ca\right)}=\frac{ab+bc+ca}{2}\)
Lại có : \(\frac{ab+bc+ca}{2}\ge\frac{3\sqrt{a^3b^3c^3}}{2}=\frac{3}{2}\)
Do đó : \(M\ge\frac{3}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c=1\)
Ta có : \(\frac{1}{a^3\left(b+c\right)}=\frac{\frac{1}{a^2}}{a\left(b+c\right)}=\frac{\left(\frac{1}{a}\right)^2}{a\left(b+c\right)}\)
Tương tự : \(\frac{1}{b^3\left(a+c\right)}=\frac{\left(\frac{1}{b}\right)^2}{b\left(a+c\right)}\) , \(\frac{1}{c^3\left(a+b\right)}=\frac{\left(\frac{1}{c}\right)^2}{c\left(a+b\right)}\)
Ta thấy : \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Leftrightarrow\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\)
Áp dụng BĐT Svacxo ta có :
\(M=\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^2\left(a+c\right)}+\frac{1}{c^3\left(a+b\right)}\ge\frac{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{b}\right)^2}{2\left(ab+bc+ca\right)}=\frac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)}\) \(\ge\frac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\frac{3}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c=1\)
Vâỵ \(M_{min}=\frac{3}{2}\) tại \(a=b=c=1\)

Có ![]()
![]() và tứ diện O.ABC vuông tại O nên:
và tứ diện O.ABC vuông tại O nên:
![]()

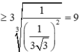
![]()
Chọn đáp án B. Mẹo TN: Vì tính đối xứng cho

![]()
Chọn đáp án B.

Ta có: \(\sqrt[3]{\left(a+b\right).\frac{2}{3}.\frac{2}{3}}\le\frac{a+b+\frac{4}{3}}{3}=\frac{a+b}{3}+\frac{4}{9}\)
Tương tự rồi cộng các vế của BĐT lại, ta được: \(\sqrt[3]{\frac{4}{9}}P\le\frac{2\left(a+b+c\right)}{3}+\frac{4}{3}=2\Rightarrow P\le\sqrt[3]{18}\)
Đẳng thức xảy ra khi \(a=b=c=\frac{1}{3}\)
Theo bđt bunhiacopxki
\(P\le\left(1+1+1\right)\left(a+b+b+c+c+a\right)=6\left(a+b+c\right)=18\)
Dấu ''='' xảy ra khi a = b = c = 1
quên ct, làm lại bài nhé
Theo bđt bunhiacopxki
\(P^2=\left(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\right)^2\le\left(1+1+1\right)\left(2a+2b+2c\right)=6.3=18\Rightarrow P=\sqrt{18}=3\sqrt{2}\)
Dấu ''='' xảy ra khi a = b = c = 1