Mọi người giúp mình bài 4 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 12 2021
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)
21 tháng 7 2021
a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=\dfrac{81}{4}+36=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\dfrac{81}{4}}{\dfrac{15}{2}}=\dfrac{27}{10}\)cm
=> \(CH=BC-BH=\dfrac{15}{2}-\dfrac{27}{10}=\dfrac{24}{5}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}\)
\(=\dfrac{4,5.6}{\dfrac{15}{2}}=\dfrac{18}{5}\)cm
AT
21 tháng 7 2021
tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=\left(4,5\right)^2+6^2=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}=7,5\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\left(4,5\right)^2}{7,5}=\dfrac{27}{10}=2,7\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{6^2}{7,5}=\dfrac{24}{5}=4,8\left(cm\right)\)
NN
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 6 2023
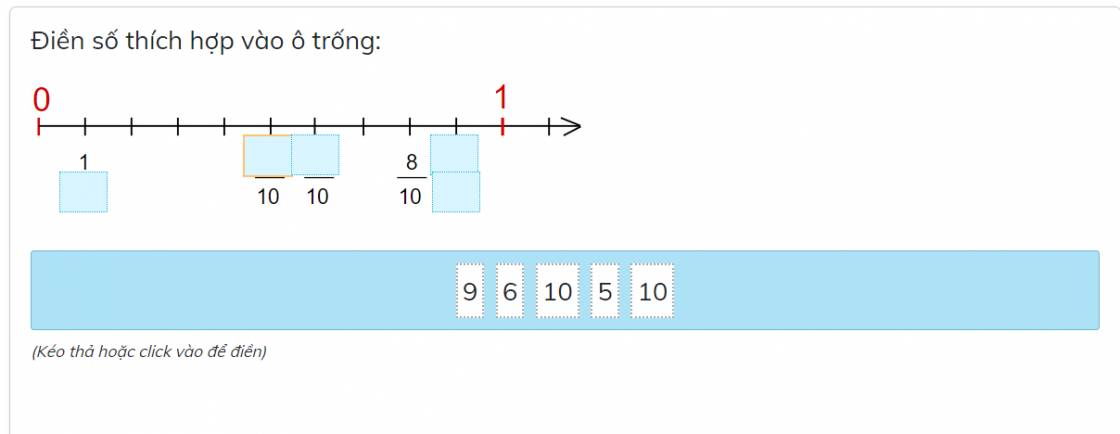
Từ 0 đến 1 được chia thành 10 phần bằng nhau.
Giá trị của mỗi phần là: \(\dfrac{1}{10}\)
Từ lập luận trên ta có:
Số thích hợp để điền vào các ô trống lần lượt là:
10; 5; 6; 9; 10
5 tháng 6 2023
0 ; 1/10 ; 2/10 ; 3/10 ; 4/10 ; 5/10 ; 6/10 ; 7/10 ; 8/10 ; 9/10 ; 1
Chúc bạn học tốt!
K
13 tháng 12 2020
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
K
13 tháng 12 2020
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
NC
1
Bài 4:
a: Xét tứ giác BGCH có
M là trung điểm của GH
M là trung điểm của BC
Do đó; BGCH là hình bình hành
SUy ra: BG//CH
b: Xét ΔBMK vuông tại M và ΔCMJ vuông tại M có
MB=MC
\(\widehat{MBK}=\widehat{MCJ}\)
Do đó: ΔBMK=ΔCMJ
Suy ra: BK=CJ