Mng giúp em vs ạ em cảm ơn 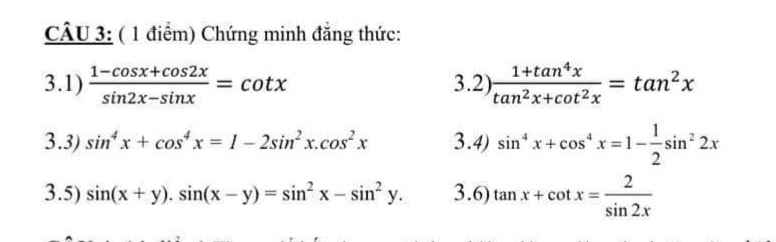
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5


Bài 1:
1. \(NaOH+HNO_3\rightarrow NaNO_3+H_2O\)
\(Ba\left(OH\right)_2+2HNO_3\rightarrow Ba\left(NO_3\right)_2+2H_2O\)
\(Fe\left(OH\right)_3+3HNO_3\rightarrow Fe\left(NO_3\right)_3+3H_2O\)
2. \(2NaOH+CO_2\rightarrow Na_2CO_3+H_2O\)
\(Ba\left(OH\right)_2+CO_2\rightarrow BaCO_3+H_2O\)
Bạn tham khảo nhé!
Bài 2:
Ta có: \(m_{NaOH}=100.4\%=4\left(g\right)\Rightarrow n_{NaOH}=\dfrac{4}{40}=0,1\left(mol\right)\)
PT: \(NaOH+HCl\rightarrow NaCl+H_2O\)
_____0,1_____0,1 (mol)
\(\Rightarrow a=C_{M_{HCl}}=\dfrac{0,1}{0,02}=5M\)
Bài 3:
Ta có: \(m_{NaOH}=100.8\%=8\left(g\right)\Rightarrow n_{NaOH}=\dfrac{8}{40}=0,2\left(mol\right)\)
\(m_{MgSO_4}=60.10\%=6\left(g\right)\Rightarrow n_{MgSO_4}=\dfrac{6}{120}=0,05\left(mol\right)\)
PT: \(2NaOH+MgSO_4\rightarrow Na_2SO_4+Mg\left(OH\right)_{2\downarrow}\)
Xét tỉ lệ: \(\dfrac{0,2}{2}>\dfrac{0,05}{1}\), ta được NaOH dư.
Theo PT: \(\left\{{}\begin{matrix}n_{NaOH\left(pư\right)}=2n_{MgSO_4}=0,1\left(mol\right)\\n_{Na_2SO_4}=n_{Mg\left(OH\right)_2}=n_{MgSO_4}=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow n_{NaoH\left(dư\right)}=0,1\left(mol\right)\)
Ta có: m dd sau pư = 100 + 60 - 0,05.58 = 157,1 (g)
\(\Rightarrow\left\{{}\begin{matrix}C\%_{NaOH\left(dư\right)}=\dfrac{0,1.40}{157,1}.100\%\approx2,55\%\\C\%_{Na_2SO_4}=\dfrac{0,05.142}{157,1}.100\%\approx4,52\%\end{matrix}\right.\)
Bạn tham khảo nhé!

Diện tích tấm bìa là: \(\dfrac{3}{4}\times\dfrac{1}{2}=\dfrac{3}{8}\left(m^2\right)\)
Diện tích tấm bìa còn lại: \(\dfrac{3}{8}\times\left(1-\dfrac{2}{3}\right)=\dfrac{1}{8}\left(m^2\right)\)

Gọi nhiệt độ cân bằng là \(t\left(t_2< t< t_3\right)\)
Giả sử \(t>t_1\Rightarrow Q_{thu}=Q_1+Q_2;Q_{tỏa}=Q_3\)
\(Q_{thu}=Q_{tỏa}\)
\(\Leftrightarrow Q_1+Q_2=Q_3\)
\(\Leftrightarrow m_1.C_1.\left(t-t_1\right)+m_2.C_2.\left(t-t_2\right)=m_3.C_3.\left(t_3-t\right)\)
\(\Leftrightarrow2000.\left(t-6\right)+10.4000.\left(t+40\right)=5.2000.\left(60-t\right)\)
\(\Leftrightarrow t=-19^oC\) (Trái với giả sử)
\(\Rightarrow t< t_1\Rightarrow Q_{thu}=Q_2;Q_{tỏa}=Q_1+Q_3\)
\(Q_{thu}=Q_{tỏa}\)
\(\Leftrightarrow m_2.C_2.\left(t-t_2\right)=m_1.C_1.\left(t-t_1\right)+m_3.C_3.\left(t_3-t\right)\)
\(\Leftrightarrow10.4000.\left(t+40\right)=2000.\left(t-6\right)+5.2000.\left(60-t\right)\)
\(\Leftrightarrow t=-19^oC\)
Kết luận: Nhiệt độ khi cân bằng là \(t=-19^oC\)


 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
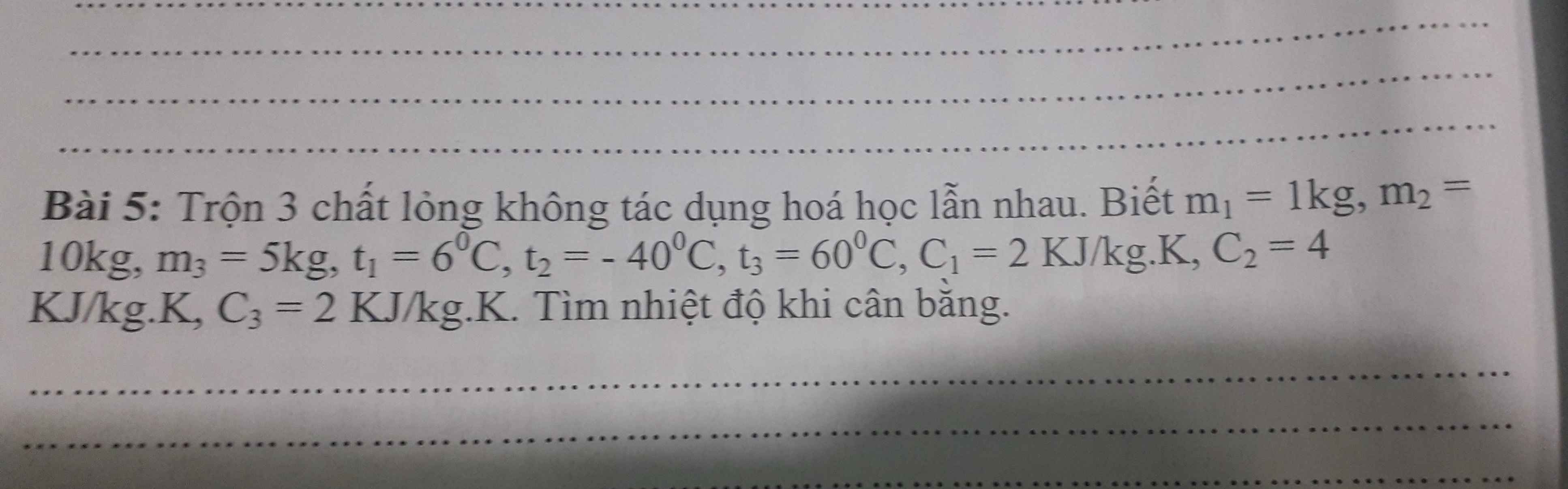
1.
\(\dfrac{1-cosx+cos2x}{sin2x-sinx}=\dfrac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}\)
\(=\dfrac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}=\dfrac{cosx}{sinx}=cotx\)
2.
\(\dfrac{1+tan^4x}{tan^2x+cot^2x}=\dfrac{1+tan^4x}{tan^2x+\dfrac{1}{tan^2x}}=\dfrac{1+tan^4x}{\dfrac{tan^4x+1}{tan^2x}}=tan^2x\)
3.
\(sin^4x+cos^4x=sin^4x+cos^4x+2sin^2x.cos^2x-2sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-2sin^2x.cos^2x\)
4.
Áp dụng câu 3:
\(sin^4x+cos^4x=1-2sin^2x.cos^2x\)
\(=1-\dfrac{1}{2}\left(2sinx.cosx\right)^2\)
\(=1-\dfrac{1}{2}sin^22x\)
5.
\(sin\left(x+y\right)sin\left(x-y\right)=\dfrac{1}{2}cos\left[\left(x-y\right)-\left(x+y\right)\right]-\dfrac{1}{2}cos\left[\left(x-y\right)+\left(x+y\right)\right]\)
\(=\dfrac{1}{2}\left(cos2y-cos2x\right)=\dfrac{1}{2}\left(1-2sin^2y\right)-\dfrac{1}{2}\left(1-2sin^2x\right)\)
\(=sin^2x-sin^2y\)
6.
\(tanx+cotx=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}\)
\(=\dfrac{1}{sinx.cosx}=\dfrac{2}{2sinx.cosx}=\dfrac{2}{sin2x}\)