Cho hình chữ nhật ABCD có AB=20cm BC=30cm
Xác định vị trí các đỉnh hình bình hành MNP
sao cho M thuộc BC N thuộc AB Q thuộc DC và MB=NB=QD=DP để diện tích MNPQ lớn nhất,
giá trị lớn nhất đó là bao nhiêu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ∆ ABC đồng dạng với ∆ AMN nên:
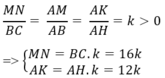
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
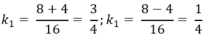
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
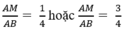

Vì ∆ ABC đồng dạng với ∆ AMN nên:
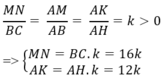
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
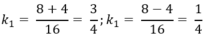
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
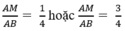

cái hình thì mk gửi link trong ib nhé
a) Gọi O là giao điểm của AC và BD
\(\Delta OAB\) vuông tại O có \(OA^2+OB^2=AB^2=49\)
Lại có: \(\tan BAC=\tan OAB=\frac{OB}{OA}=\frac{3}{4}\)\(\Leftrightarrow\)\(\frac{OA^2}{16}=\frac{OB^2}{9}=\frac{OA^2+OB^2}{16+9}=\frac{49}{25}\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{OA}{4}=\frac{7}{5}\\\frac{OB}{3}=\frac{7}{5}\end{cases}}\Leftrightarrow\hept{\begin{cases}OA=\frac{28}{5}\left(cm\right)\\OB=\frac{21}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(\hept{\begin{cases}AC=2OA=\frac{56}{5}\left(cm\right)\\BD=2OB=\frac{42}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.\frac{56}{5}.\frac{42}{5}=\frac{1176}{25}=47,04\left(cm^2\right)\)
b) Gọi E, F lần lược là giao điểm của BD với MN và PQ
tam giác ABD có MQ // BD
\(\Rightarrow\)\(\frac{MQ}{BD}=\frac{MA}{AB}\) ( hệ quả định lí Talet )
tam giác OAD có QF // OA
\(\Rightarrow\)\(\frac{QF}{OA}=\frac{DQ}{AQ}=\frac{MB}{AB}\) ( hệ quả định lí Talet )
\(\Rightarrow\)\(\frac{MQ}{BD}+\frac{QF}{OA}=\frac{MA+MB}{AB}=1\)
\(\Rightarrow\)\(1\ge2\sqrt{\frac{MQ.QF}{BD.OA}}\)\(\Leftrightarrow\)\(MQ.QF\le\frac{1}{4}BD.OA\)
Tương tự, ta cũng có: \(NP.PF\le\frac{1}{4}BD.OC\)
\(\Rightarrow\)\(MQ.QF+NP.PF=S_{MEFQ}+S_{NEFP}=S_{MNPQ}\le\frac{1}{4}BD.AC=\frac{1}{2}S_{ABCD}=23,52\left(cm^2\right)\)
Dấu "=" xảy ra khi M, N, P, Q là trung điểm của AB, BC, CD, DA