Trên mặt phẳng cho 11 đường thẳng cắt nhau từng đôi một . CMR : Luôn luôn có 1 góc tạo thành nhỏ hơn 17 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



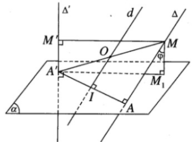
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

Ta chọn điểm O bất kì nằm trong mặt phẳng chứa 5 đường thẳng ấy. Qua O ta dựng các đường thẳng song song với các đường thẳng đã cho , khi đó có 10 góc đôi một đối đỉnh qua O . Vậy sẽ có ít nhất một góc không vượt quá \(\frac{180^o}{5}=36^o\)
Gọi O là một điểm trên mặt phẳng . Qua O dựng các đường thẳng song song với 11 đường thẳng đã cho.Tại O có 22 góc đôi một đối đỉnh có tổng bằng 360 độ. Suy ra luôn có một góc tạo thành nhỏ hơn \(\frac{360^o}{11}< 17^o\) (đpcm)
Mình sửa lại một chút , phải là \(\frac{180^o}{11}< 17^o\) nhé :)