1 thỏi hợp kim chì , kẽm có khối lượng 500g ở \(100^0C\)được thả vào 1 nhiệt lượng kế có nhiệt dung \(300J/^0\)chứa 1kg nước ở \(20^0C\), nhiệt độ cân bằng là \(22^0C\). Tìm khối lượng chì, kẽm có trong hợp kim , biết nhiệt dung riêng của chì \(130J/^0\), nhiệt dung riêng của kẽm là 400J, nước 4200J
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhiệt lượng thu vào của nhiệt lượng kế & nước là ( cho mnlk = 8,5 )
\(Q_{thu}=\left(1.300+1.4200\right)\left(32,5-30\right)=11250J\)
Ta có phương trình cân bằng nhiệt
\(Q_{thu}=Q_{toả}=16875J\)
Nhiệt lượng chì và kẽm lần lượt toả ra là
\(Q_1=m_1130.\left(120-32,5\right)=m_111375J\\ Q_2=0,5-m_1.400\left(120-32,5\right)=0,5-m_1.35000J\)
Ta có
\(Q_1+Q_2=Q_{toả}\\ m_1.11375+0,5-m_1.35000=16875\)
Giải phương trình trên ta được
\(\Leftrightarrow\left\{{}\begin{matrix}m_1\approx0,026\\m_2\approx0,474\end{matrix}\right.\)

Nhiệt lượng do thỏi hợp kim tỏa ra:
\(Q_1+Q_2=\left(m_1c_1+m_2c_2\right)\left(t_1-t\right)\)
\(=\left(130m_1+400m_2\right)\left(125-25\right)\)
\(=100.\left(130m_1+400m_2\right)J\)
Nhiệt lượng do nhiệt lượng kế và nước thu vào:
\(Q_3+Q_4=\left(m_3c_3+m_4c_4\right)\left(t-t_2\right)\)
\(=\left(1,6\cdot250+1\cdot4200\right)\left(25-20\right)\)
\(=23000J\)
Ta có phương trình cân bằng nhiệt:
\(Q_1+Q_2=Q_3+Q_4\)
\(\Rightarrow100\left(130m_1+400m_2\right)=23000\)
\(\Rightarrow13m_1+40m_2=23\)
Mà \(m_1+m_2=1\)
\(\Rightarrow\left\{{}\begin{matrix}m_1=0,63kg\\m_2=0,37kg\end{matrix}\right.\)
\(\%m_1=\dfrac{0,63}{1}\cdot100\%=63\%\)
\(\%m_2=100\%-63\%=37\text{%}\)

Đáp án: B
Phương trình cân bằng nhiệt:
(Cnlk + mncn).(t – t1) = [mkck + (mhk – mk)cch].(t2 – t)
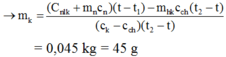
→ mch = mhk – mk = 5 g.

Nhiệt lượng toả ra :
Q = m 1 c 1 ∆ t + (0,05 - m1 ) c 2 ∆ t (1)
Ở đây m 1 , c 1 là khối lượng và nhiệt dung riêng của kẽm, c 2 là nhiệt dung riêng của chì.
Nhiệt lượng thu vào :
Q' = mc ∆ t' + c' ∆ t' = (mc + c') ∆ t' (2)
Ở đây m, c là khối lượng và nhiệt dung riêng của nước, c' là nhiệt dung riêng của nhiệt lượng kế.
Từ (1) và (2) rút ra :
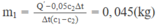
Khối lượng của chì m 2 = 0,05 – m 1 , hay m 2 = 0,005 kg.

Gọi t1 là nhiệt độ ban đầu của miếng hợp kim, ta có t1=1240C
t2 là nhiệt độ ban đầu của nhiệt lượng kế và nước trong nhiệt lượng kế, ta có t2=160C
t=320C - nhiệt độ khi cân bằng trong nhiệt lượng kế
Nhiệt lượng toả ra:
Q Z n = m Z n . C Z n ( t 1 − t ) Q P b = m P b . C P b ( t 1 − t ) ⇔ = m Z n .337. ( 124 − 18 ) = 35722 m Z n = m P b .126. ( 124 − 18 ) = 13356 m P b
Nhiệt lượng thu vào:
Q H 2 O = m H 2 O . C H 2 O ( t − t 2 ) Q N L K = C ' ( t − t 2 ) ⇔ = 250 1000 .4180 ( 18 − 16 ) = 2090 J = 50. ( 18 − 16 ) = 100 J
Ta có, phương trình cân bằng nhiệt:
Q t o a = Q t h u ↔ 35722 m Z n + 13356 m P b = 2090 + 100 1
Mặt khác, theo đầu bài, ta có:
m Z n + m P b = 150 g = 0 , 15 k g 2
Từ (1) và (2), ta có:
35722 m Z n + 13356 m P b = 2190 m Z n + m P b = 0 , 15 → m Z n ≈ 8.10 − 3 k g m P b = 0 , 142 k g
Đáp án: A

Gọi m1 là khối lượng của chì, m2 là khối lượng của kẽm, m là khối lượng của hợp kim:
m = m1 + m2 = 0,05kg (1)
Nhiệt lượng chì và kẽm tỏa ra:
Q1 = m1.c1.(t0 - t) = m1.130.(136 – 18) = 15340.m1
Q2 = m2.c2.(t0 - t) = m2.210.(136 – 18) = 24780.m2
Nhiệt lượng nước thu vào:
Qn = mn.cn.(t - tn) = 0,05.4200.(18 - 14) = 810J
Vì muốn cho nhiệt lượng kế nóng thêm lên 1oC thì cần 65,1J nên nhiệt lượng kế thu vào:
Q4 = Qk.(t – tn) = 65,1.(18 – 14) = 260,4J
Vì nhiệt lượng tỏa ra bằng nhiệt lượng thu vào nên: Q3 + Q4 = Q1 + Q2
↔ 15340.m1 + 24780.m2 = 1100,4 (2)
Từ (1), rút m2 = 0,05 – m1, thay vào phương trình (2), giải ra ta được:
m1 = 0,015kg, suy ra m2 = 0,035kg
Vậy khối lượng chì là 15 gam và khối lượng kẽm là 35 gam.

Theo đề bài ta đc
\(m_1+m_2=0,1\\ \Rightarrow m_2=0,1-m_1\)
Ta có ptcbn
\(Q_{thu}=Q_{tỏa}\\ \Leftrightarrow0,1.4200\left(18-14\right)=m_1.210+\left(100-m_1\right)130\left(136-14\right)\\ \Rightarrow\left\{{}\begin{matrix}m_1\approx0,04\\m_2\approx0,06\end{matrix}\right.\)
