Tính giá trị của đa thức P(x)= x6-6x5+6x4-6x3+6x2-6x+1 tại x=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 3 2017
Biểu thức xác định khi x 2 - 36 ≠ 0 , x 2 + 6 x ≠ 0 , 6 – x ≠ 0 và 2x – 6 ≠ 0
x 2 - 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x 2 + 6 x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
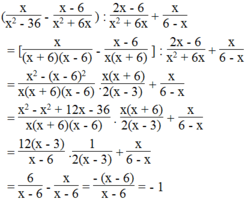
Vậy biểu thức không phụ thuộc vào biến x.
CM
4 tháng 11 2018
Đáp án C.
⇒ Chia 2 vế phương trình cho x 3 ta được:
x 3 + 1 x 3 + 3 x 2 + 1 x 2 + 6 x + 1 x = m (*)
Đặt t = x + 1 x ⇒ t ≥ 2 , phương trình (*) m = t 3 + 3 t 2 + t - 6
Xét f ( t ) = t 3 + 3 t 2 + 3 t - 6 trên ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
f ' ( t ) = 0 ⇔ t = - 1
Bảng biến thiên:
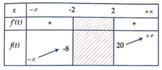
⇒ f ( t ) ∈ ( - ∞ ; - 8 ] ∪ [ 20 ; + ∞ ) ∀ t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
⇒ Phương trình f (t) vô nghiệm ⇔ m ∈ - 8 ; 20
⇒ Có 27 giá trị m nguyên thỏa mãn.
CN
34
17 tháng 5 2022
a: \(P\left(x\right)=-5x^3+3x^2+2x+5\)
\(Q\left(x\right)=-5x^3+6x^2+2x+5\)
b: Q(x)-P(x)=6
\(\Leftrightarrow-5x^3+6x^2+2x+5+5x^3-3x^2-2x-5=6\)
=>3x2=6
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
17 tháng 5 2022
P(x)=15 - 4x3 + 3x2 + 2x - x3 - 10
và Q(x)=5 + 4x3 + 6x2 - 5x - 9x3 + 7x
a) P(x)= -5x^3 + 3x^2 + 2x + 5.
Q(x)= -5x^3 + 6x^2 + 2x + 5.
b)
P(x)= -5x^3 + 3x^2 + 2x + 5 tại x= 1/2.
P(x)= -5 . 1/2^3 + 3 . 1/2^2 + 2 . 1/2 +5 = 49/8.
Q(x)= -5x^3 + 6x^2 + 2x + 5 tại x= 1/2
Q(x)= -5 . 1/2^3 + 6 . 1/2^2 + 2 . 1/2 +5= 55/8.
c)
P(x) - Q(x)= (-5x^3 + 3x^2 + 2x + 5) - (-5x^3 + 6x^2 + 2x + 5)
Kết quả -3x^2.
Nhớ nhấn like đấy
26 tháng 12 2021
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
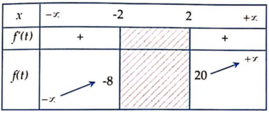
\(P\left(x\right)=5^6-6.5^5+6.5^4-6.5^3+6.5^2-6.5+1=5^6-6\left(5^5-5^4-5^3-5^2-5\right)+1=1556\)
mình quên là k dùng máy tính bỏ túi nha