CHO AOB = 80. GỌI AOC VÀ BOD LA F CÁC GÓC KỀ BÙ AOB. GỌI OM, ON LẦN LƯỢT LÀ TIA PHÂN GIÁC CỦA BOD VÀ AOC. CHỨNG MINH RẰNG HAI TIA OM VÀ ON ĐỐI NHAU.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
EG
31 tháng 7 2018
(tự vẽ hình)
a) Vì góc BOD và góc AOB là hai góc đối đỉnh nên \(\widehat{BOD}=180^o-\widehat{AOB}=180^o-80^o=100^o\) (3)
=> Tia OA và tia OD đối nhau.(1)
Vì góc AOC và góc AOB là hai góc đối đỉnh nên \(\widehat{AOC}=180^o-\widehat{AOB}=180^o-80^o=100^o\) (4)
=> Tia OB và tia OC đối nhau.(2)
Từ (1);(2);(3);(4) suy ra: góc AOC và góc BOD là hai góc đối đỉnh.
b) Xét: Tia Om, On lần lượt là tia phân giác của góc AOC, BOD.
- Vì tia Om là tia phân giác của góc AOC nên góc COm=MOA=1/2. AOC.
- Vì tia ON là tia phân giác của góc BOD nên góc BOn=DOn=1/2.DOB.
Mà góc AOC = DOB => COm= BOn
Vì CO và OB là hai tia đối nhau
=> \(\widehat{COm}+\widehat{mOB}=180^o\)
=> \(\widehat{COn}+\widehat{BOn}=180^o\)
=> \(\widehat{COm}+\widehat{BOn}=180^o\)
hay Tia Om và On là 2 tia đối nhau.
Chúc cậu học tốt!
5 tháng 8 2015
a) Vì góc AOC kề bù với góc AOB => OC và OB là 2 tia đối nhau và góc AOC + AOB = 1800
Vì góc BOD và AOB là 2 tia đối nhau => OA và OD là 2 tia đối nhau và góc BOD + AOB = 180o
=> góc AOC = BOD
Góc AOC và BOD có OA là tia đối của tia OD; OC là tia đối của tia OB; góc AOC = BOD
=> góc AOC và BOD là 2 góc đối đỉnh
b) gọi Ot là tia p/g của góc BOD => góc O1 = O2 = góc BOD/2
Gọi Ot' là tia đối của tia Ot có OB là tia đối của tia OC => góc O1 = O4 (đối đỉnh)
Tia OD là tia đối của tia OA => góc O2 = O3 (đối đỉnh)
=> O3 = O4 = BOD/2 = AOC /2 => Ot' là tia phân giác của góc AOC
Mà Ot và Ot' đối nhau tức là chúng cùng nằm trên 1 đường thẳng
=> điều phải chứng minh
T
10 tháng 8 2018
a) Vì góc AOC kề bù với góc AOB => OC và OB là 2 tia đối nhau và góc AOC + AOB = 1800
Vì góc BOD và AOB là 2 tia đối nhau => OA và OD là 2 tia đối nhau và góc BOD + AOB = 180o
=> góc AOC = BOD
Góc AOC và BOD có OA là tia đối của tia OD; OC là tia đối của tia OB; góc AOC = BOD
=> góc AOC và BOD là 2 góc đối đỉnh
b) gọi Ot là tia p/g của góc BOD => góc O1 = O2 = góc BOD/2
Gọi Ot' là tia đối của tia Ot có OB là tia đối của tia OC => góc O1 = O4 (đối đỉnh)
Tia OD là tia đối của tia OA => góc O2 = O3 (đối đỉnh)
=> O3 = O4 = BOD/2 = AOC /2 => Ot' là tia phân giác của góc AOC
Mà Ot và Ot' đối nhau tức là chúng cùng nằm trên 1 đường thẳng
=> điều phải chứng minh
26 tháng 9 2021
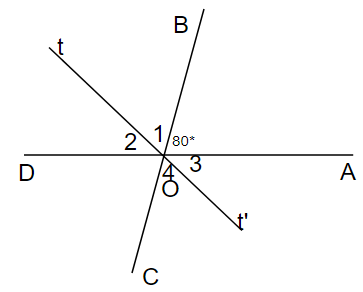
a) Vì ∠AOC kề bù với ∠AOB
⇒ OC và OB là 2 tia đối nhau và ∠AOC + ∠AOB = 1800
Vì ∠BOD và ∠AOB là 2 tia đối nhau
⇒ OA và OD là 2 tia đối nhau và ∠BOD + ∠AOB = 180o
⇒ ∠AOC = ∠BOD
Vì ∠AOC có OA là tia đối của tia OD;
∠BOD có OC là tia đối của tia OB
Mà ∠AOC = ∠BOD
⇒ ∠AOC và ∠BOD là 2 góc đối đỉnh
b) Gọi Ot là tia phân giác của ∠BOD
⇒ ∠O1 = ∠O2 = ∠BOD/2
Gọi Ot' là tia đối của tia Ot có OB là tia đối của tia OC
⇒ ∠O1 = ∠O4 (đối đỉnh)
Tia OD là tia đối của tia OA
⇒ ∠O2 = ∠O3 (đối đỉnh)
⇒ ∠O3 = ∠O4 = ∠BOD/2 = ∠AOC /2
⇒ Ot' là tia phân giác của ∠AOC
Mà Ot và Ot' đối nhau
⇒ Ot và Ot' cùng nằm trên 1 đường thẳng (đpcm)
